题目内容
11.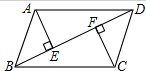 如图,BD是?ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:AE=CF.
如图,BD是?ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:AE=CF.
分析 根据平行四边形的性质得出AB=CD,AB∥CD,根据平行线的性质得出∠ABE=∠CDF,求出∠AEB=∠CFD=90°,根据AAS推出△ABE≌△CDF,得出对应边相等即可.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
$\left\{\begin{array}{l}{∠AEB=∠CFD}&{\;}\\{∠ABE=∠CDF}&{\;}\\{AB=CD}&{\;}\end{array}\right.$,
∴△ABE≌△CDF(AAS),
∴AE=CF.
点评 本题考查了平行四边形的性质,平行线的性质,全等三角形的性质和判定的应用;证明△ABE≌△CDF是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.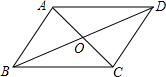 如图,在?ABCD中,对角线AC与BD交于点O,若增加一个条件,使?ABCD成为菱形,下列给出的条件不正确的是( )
如图,在?ABCD中,对角线AC与BD交于点O,若增加一个条件,使?ABCD成为菱形,下列给出的条件不正确的是( )
 如图,在?ABCD中,对角线AC与BD交于点O,若增加一个条件,使?ABCD成为菱形,下列给出的条件不正确的是( )
如图,在?ABCD中,对角线AC与BD交于点O,若增加一个条件,使?ABCD成为菱形,下列给出的条件不正确的是( )| A. | AB=AD | B. | AC⊥BD | C. | AC=BD | D. | ∠BAC=∠DAC |
2.据《南国早报》报道:2016年广西高考报名人数约为332000人,创历史新高,其中数据332000用科学记数法表示为( )
| A. | 0.332×106 | B. | 3.32×105 | C. | 3.32×104 | D. | 33.2×104 |
19.方程2x+3=7的解是( )
| A. | x=5 | B. | x=4 | C. | x=3.5 | D. | x=2 |
7.下列定理中,没有逆定理的是( )
| A. | 直角三角形的两锐角互余 | |
| B. | 同位角相等,两直线平行 | |
| C. | 对顶角相等 | |
| D. | 直角三角形两直角边平方和等于斜边的平方 |
 如图,△ABC中,∠C=90°,AC=3,BC=4,AB的垂直平分线交AB于E,交BC于D,求BD的长.
如图,△ABC中,∠C=90°,AC=3,BC=4,AB的垂直平分线交AB于E,交BC于D,求BD的长.