题目内容
5．
有理数a，b在数轴上的位置如图所示，则|a+b|+|a-b|化简的结果为（ ）| A． | -2b | B． | -2a | C． | 2b | D． | 0 |
分析 根据数轴上点的位置判断出绝对值里边式子的正负，利用绝对值的代数意义化简，去括号合并即可得到结果．
解答 解：根据数轴上点的位置得：b＜0＜a，且|a|＜|b|，
∴a+b＜0，a-b＞0，
则原式=-a-b+a-b=-2b，
故选A
点评 此题考查了整式的加减，数轴，以及绝对值，判断出绝对值里边式子的正负是解本题的关键．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
如图，BD是∠ABC的平分线，DE∥CB，交AB于点E，∠BED=150°，∠BDC=60°．求∠A的度数．
13．
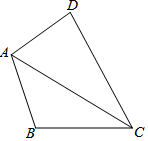如图，四边形ABCD中，AB=AD，∠B+∠D=180°，若AC=12，则四边形ABCD的面积最大值为（ ）
如图，四边形ABCD中，AB=AD，∠B+∠D=180°，若AC=12，则四边形ABCD的面积最大值为（ ）| A． | 36 | B． | $36\sqrt{2}$ | C． | 72 | D． | $72\sqrt{2}$ |
20．
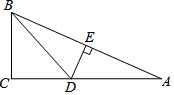如图，在Rt△ABC中，∠C=90°，把AB对折后，点A与点B重合，折痕为DE，若BC=2，AC=4，则BD=（ ）
如图，在Rt△ABC中，∠C=90°，把AB对折后，点A与点B重合，折痕为DE，若BC=2，AC=4，则BD=（ ）| A． | $\frac{3}{2}$ | B． | 2 | C． | $\frac{5}{2}$ | D． | 3 |
10．若代数式-3a-x+1by-2与2a2x-2b是同类项，则x-y的值为（ ）
| A． | -2 | B． | 2 | C． | -3 | D． | 3 |
如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．求证：AF=2CD．