题目内容
15. 如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:AF=2CD.
如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:AF=2CD.
分析 只要证明Rt△AEF≌Rt△CEB,推出AF=CB,又AB=AC,AD⊥BC,推出CD=BD,由此即可证明.
解答 证明:在Rt△AEF和Rt△CEB中,
有$\left\{\begin{array}{l}{AE=AE}\\{∠AEF=∠CEB=90°}\\{∠EAF=∠ECB}\end{array}\right.$,
∴Rt△AEF≌Rt△CEB,
∴AF=CB,
又∵AB=AC,AD⊥BC,
∴CD=BD,
∴CF=2CD.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
5. 有理数a,b在数轴上的位置如图所示,则|a+b|+|a-b|化简的结果为( )
有理数a,b在数轴上的位置如图所示,则|a+b|+|a-b|化简的结果为( )
 有理数a,b在数轴上的位置如图所示,则|a+b|+|a-b|化简的结果为( )
有理数a,b在数轴上的位置如图所示,则|a+b|+|a-b|化简的结果为( )| A. | -2b | B. | -2a | C. | 2b | D. | 0 |
20.已知圆锥的底面半径为3,母线长为8,则圆锥的侧面积为( )
| A. | 48π | B. | 46π | C. | 36π | D. | 24π |
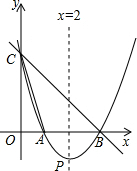 如图,直线y=-x+3与x轴、y轴分别相交于点B、C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一个交点为A,顶点为P,且对称轴为直线x=2.
如图,直线y=-x+3与x轴、y轴分别相交于点B、C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一个交点为A,顶点为P,且对称轴为直线x=2.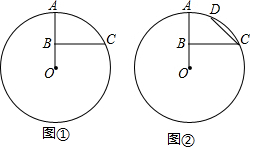 已知,点B是半径OA的中点,过点B作BC⊥OA交⊙O于点C.
已知,点B是半径OA的中点,过点B作BC⊥OA交⊙O于点C.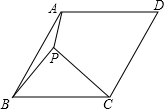 如图,菱形ABCD的边长为4,∠ABC=60°,在菱形ABCD内部有一点P,当PA+PB+PC值最小时,PB的长为$\frac{4\sqrt{3}}{3}$.
如图,菱形ABCD的边长为4,∠ABC=60°,在菱形ABCD内部有一点P,当PA+PB+PC值最小时,PB的长为$\frac{4\sqrt{3}}{3}$.