题目内容
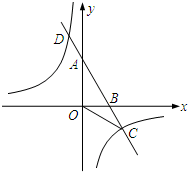 如图,已知A、B两点的坐标分别为A(0,2
如图,已知A、B两点的坐标分别为A(0,2| 3 |
| m |
| x |
(1)求反比例函数的解析式;
(2)分别求∠BOC、∠ACO的度数.
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)先利用待定系数法确定直线AB的解析式为y=-
x+2
;再把D(-1,a)代入y=-
x+2
求出a确定D点坐标为(-1,3
),然后把D点坐标代入y=
求出m,则可得到反比例函数解析式为y=-
;
(2)先解方程组
得到C点坐标为(3,-
),作CH⊥x轴于H,在Rt△OCH中,利用正切的定义可得到∠COH=30°,则∠AOC=90°+∠BOC=120°,再计算OA和OC的长得到OA=OC,于是∠ACO=
(180°-120°)=30°.
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| m |
| x |
3
| ||
| x |
(2)先解方程组
|
| 3 |
| 1 |
| 2 |
解答: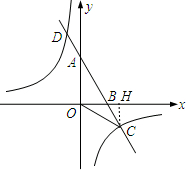 解:(1)设直线AB的解析式为y=kx+b,
解:(1)设直线AB的解析式为y=kx+b,
把A(0,2
),B(2,0)代入得
,解得
,
所以直线AB的解析式为y=-
x+2
;
把D(-1,a)代入y=-
x+2
得a=3
,则D点坐标为(-1,3
),
把D(-1,3
)代入y=
得m=-1×3
=-3
,
所以反比例函数解析式为y=-
;
(2)解方程组
得
或
,
所以C点坐标为(3,-
),
把x=0代入y=-
x+2
得y=2
,
所以A点坐标为(0,2
),
作CH⊥x轴于H,如图,
在Rt△OCH中,CH=
,OH=3,
tan∠COH=
,OC=2CH=2
,
所以∠COH=30°,即∠BOC=30°,
所以∠AOC=90°+∠BOC=120°,
因为OA=OC=2
,
所以∠ACO=
(180°-120°)=30°.
 解:(1)设直线AB的解析式为y=kx+b,
解:(1)设直线AB的解析式为y=kx+b,把A(0,2
| 3 |
|
|
所以直线AB的解析式为y=-
| 3 |
| 3 |
把D(-1,a)代入y=-
| 3 |
| 3 |
| 3 |
| 3 |
把D(-1,3
| 3 |
| m |
| x |
| 3 |
| 3 |
所以反比例函数解析式为y=-
3
| ||
| x |
(2)解方程组
|
|
|
所以C点坐标为(3,-
| 3 |
把x=0代入y=-
| 3 |
| 3 |
| 3 |
所以A点坐标为(0,2
| 3 |
作CH⊥x轴于H,如图,
在Rt△OCH中,CH=
| 3 |
tan∠COH=
| ||
| 3 |
| 3 |
所以∠COH=30°,即∠BOC=30°,
所以∠AOC=90°+∠BOC=120°,
因为OA=OC=2
| 3 |
所以∠ACO=
| 1 |
| 2 |
点评:本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了待定系数法确定函数解析式.

练习册系列答案
相关题目
 小明和同学去公园游玩,他们在一个平台上看见一个移动通信的信号转播铁塔,他们决定尝试着测量这个铁塔的高度,于是,小明来到平台的边缘的C处,测得仰角为45°,他们沿着台阶往下走,来到第二个平台的E处,测得仰角为30°,(其中,点A、C、D、E在同一平面上)小明和同学发现台阶共10级,每阶高20厘米,每阶宽30厘米,另测得E点到台阶的边缘D处距离为8米,请你利用上述数据求出铁塔AB的高度.(
小明和同学去公园游玩,他们在一个平台上看见一个移动通信的信号转播铁塔,他们决定尝试着测量这个铁塔的高度,于是,小明来到平台的边缘的C处,测得仰角为45°,他们沿着台阶往下走,来到第二个平台的E处,测得仰角为30°,(其中,点A、C、D、E在同一平面上)小明和同学发现台阶共10级,每阶高20厘米,每阶宽30厘米,另测得E点到台阶的边缘D处距离为8米,请你利用上述数据求出铁塔AB的高度.(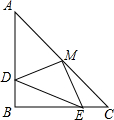 如图,在△ABC中,AB=AC,∠B=90°,D、E分别为AB、BC上的动点,且BD=CE,M是AC的中点,试探究在DE运动的过程中,△DEM的形状是否发生变化?它是什么形状的三角形?
如图,在△ABC中,AB=AC,∠B=90°,D、E分别为AB、BC上的动点,且BD=CE,M是AC的中点,试探究在DE运动的过程中,△DEM的形状是否发生变化?它是什么形状的三角形?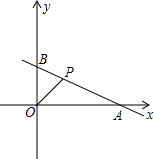 在直角坐标系中,已知点A(4,0),B(0,2),点P(x,y)在第一象限内,且x+2y=4,设△AOP的面积是S.
在直角坐标系中,已知点A(4,0),B(0,2),点P(x,y)在第一象限内,且x+2y=4,设△AOP的面积是S.  如图,已知△AOB是正三角形,OC⊥OB,将△OAB绕点O按逆时针方向旋转,使得OA与OC重合,得到△OCD,则旋转的角度是
如图,已知△AOB是正三角形,OC⊥OB,将△OAB绕点O按逆时针方向旋转,使得OA与OC重合,得到△OCD,则旋转的角度是