题目内容
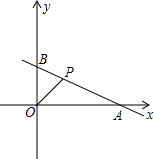 在直角坐标系中,已知点A(4,0),B(0,2),点P(x,y)在第一象限内,且x+2y=4,设△AOP的面积是S.
在直角坐标系中,已知点A(4,0),B(0,2),点P(x,y)在第一象限内,且x+2y=4,设△AOP的面积是S. (1)写出S与x之间的函数关系式,并求出x的取值范围;
(2)当S=3时,求点P的坐标;
(3)若直线OP平分△AOB的面积时,求点P的坐标.
考点:一次函数的性质
专题:
分析:(1)根据点A、P的坐标求得△AOP的底边OA与高线BC的长度;然后根据三角形的面积公式即可求得S与x的函数关系式;
(2)将S=3代入(1)中所求的式子,即可求出点P的坐标;
(3)由直线OP平分△AOB的面积,可知OP为△AOB的中线,点P为AB的中点,根据中点坐标公式即可求解.
(2)将S=3代入(1)中所求的式子,即可求出点P的坐标;
(3)由直线OP平分△AOB的面积,可知OP为△AOB的中线,点P为AB的中点,根据中点坐标公式即可求解.
解答:解:∵x+2y=4,
∴y=
(4-x),
∴S=
×4×
(4-x)=4-x,即S=4-x.
∵点P(x,y)在第一象限内,且x+2y=4,
∴
,
解得0<x<4;
(2)当S=3时,4-x=3,
解得x=1,
此时y=
(4-1)=
,
故点P的坐标为(1,
);
(3)若直线OP平分△AOB的面积,则点P为AB的中点.
∵A(4,0),B(0,2),
∴点P的坐标为(2,1).
∴y=
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
∵点P(x,y)在第一象限内,且x+2y=4,
∴
|
解得0<x<4;
(2)当S=3时,4-x=3,
解得x=1,
此时y=
| 1 |
| 2 |
| 3 |
| 2 |
故点P的坐标为(1,
| 3 |
| 2 |
(3)若直线OP平分△AOB的面积,则点P为AB的中点.
∵A(4,0),B(0,2),
∴点P的坐标为(2,1).
点评:本题考查了一次函数的性质,三角形的面积,三角形中线的性质,中点坐标公式,难度适中.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 如图,在5×5的方格(每小格边长为1)内有4只甲虫A、B、C、D,它们爬行规律总是先左右,再上下.规定:向右与向上为正,向左与向下为负.从A到B的爬行路线记为:A→B(+1,+4),从B到A的爬行路线为:B→A(-1,-4),其中第一个数表示左右爬行信息,第二个数表示上下爬行信息,那么图中
如图,在5×5的方格(每小格边长为1)内有4只甲虫A、B、C、D,它们爬行规律总是先左右,再上下.规定:向右与向上为正,向左与向下为负.从A到B的爬行路线记为:A→B(+1,+4),从B到A的爬行路线为:B→A(-1,-4),其中第一个数表示左右爬行信息,第二个数表示上下爬行信息,那么图中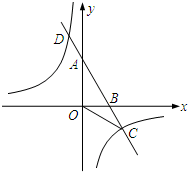 如图,已知A、B两点的坐标分别为A(0,2
如图,已知A、B两点的坐标分别为A(0,2 如图是正方体平面展开图,相对面上的两个数之和为5,则x=
如图是正方体平面展开图,相对面上的两个数之和为5,则x=