题目内容

已知a是方程x2-x-1=0的一个根，求a3-2a2+2014的值．
考点：一元二次方程的解
专题：计算题
分析：将x=a代入方程得到关系式，代入原式计算即可得到结果．
解答：解：将x=a代入方程得：a2-a-1=0，即a2=a+1，
则原式=a2（a-2）+2014
=（a+1）（a-2）+2014
=a2-a-2+2014
=a+1-a-2+2014
=2013．
点评：此题考查了一元二次方程的解，方程的解即为能使方程左右两边相等的未知数的值．
练习册系列答案
相关题目
已知：A、B、C三点的坐标分别是（-1，-1）、（5，-1）、（3，5），现A、B、C、D四点构成一个平行四边形，则顶点D的坐标为多少？
等腰三角形的两边长分别为1和2，其周长为
 
．
下列各式计算正确的是（　　）
A、x5-x3=x2
B、（mn3）3=mn6
C、（a+b）2=a2+b2
D、p6÷p2=p4（p≠0）
已知P是△ABC内一点，a，b，c为三角形的三条边，求证：PA+PB+PC＜a+b+c．
如图1，在Rt△ACB中，∠BAC=90°，AB=AC，分别过B、C两点作过点A的直线l的垂线，垂足为D、E；
（1）如图1，当D、E两点在直线BC的同侧时，猜想，BD、CE、DE三条线段有怎样的数量关系？并说明理由．
（2）如图2，当D、E两点在直线BC的两侧时，BD、CE、DE三条线段的数量关系为
 
．
（3）如图2，若直线AD被截成的线段AE、EM、MD的长度分别是a，b，c，又S△ABM=S1，S△ACM=S2，求S2-S1的值．（用含有a，b，c的代数式表示）
（4）如图3，∠BAC=90°，AB=22，AC=28．点P从B点出发沿B→A→C路径向终点C运动；点Q从C点出发沿C→A→B路径向终点B运动．点P和Q分别以每秒2和3个单位的速度同时开始运动，只要有一点到达相应的终点时两点同时停止运动；在运动过程中，分别过P和Q作PF⊥l于F，QG⊥l于G．问：点P运动多少秒时，△PFA与△QAG全等？（直接写出结果即可）
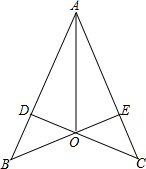如图，CD⊥AB，BE⊥AC，垂足分别为D、E，BE、CD相交于点O，∠BAO=∠CAO，求证：OB=OC．
已知：（
1
）2+1=2，S1=
1
2
；（
2
）2+1=3，S2=
2
2
；（
3
）2+1=4，S3=
3
2
．
（1）用含有n的等式表示上述变化规律；
（2）求S12+S22+S32+…+S102的值．
在△ABC中，AB=AC，BD是AC边上的中线，BD把△ABC分成两部分，已知AB+AD=13.5cm，BC+CD=11.5cm，求这个三角形的边长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网