题目内容
已知:(
)2+1=2,S1=
;(
)2+1=3,S2=
;(
)2+1=4,S3=
.
(1)用含有n的等式表示上述变化规律;
(2)求S12+S22+S32+…+S102的值.
| 1 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
(1)用含有n的等式表示上述变化规律;
(2)求S12+S22+S32+…+S102的值.
考点:规律型:数字的变化类,实数的运算
专题:
分析:(1)利用已知得出数字变化规律分别得出第n个式以及Sn的值;
(2)利用S的值,进而分别平方求出即可.
(2)利用S的值,进而分别平方求出即可.
解答:解:(1)∵(
)2+1=2,S1=
;(
)2+1=3,S2=
;(
)2+1=4,S3=
∴用含有n的等式表示上述变化规律:(
)2+1=n+1,Sn=
;
(2)S12+S22+S32+…+S102
=(
)2+(
)2+…+(
)2
=
+
+…+
=
=
.
| 1 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
∴用含有n的等式表示上述变化规律:(
| n |
| ||
| 2 |
(2)S12+S22+S32+…+S102
=(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
=
| 1 |
| 4 |
| 2 |
| 4 |
| 10 |
| 4 |
=
| 1+2+3+…+10 |
| 4 |
=
| 55 |
| 4 |
点评:此题主要考查了数字变化规律,根据题意得出数字之间的变与不变是解题关键.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
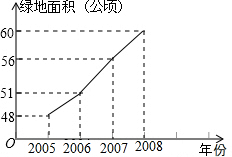 某城区近几年通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加.
某城区近几年通过拆迁旧房,植草,栽树,修建公园等措施,使城区绿地面积不断增加. 如图,已知△ABC在坐标平面内的顶点C(2,0),∠ACB=90°,∠B=30°,AB=6
如图,已知△ABC在坐标平面内的顶点C(2,0),∠ACB=90°,∠B=30°,AB=6