题目内容
9.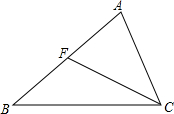 如图,F是△ABC的AB边上一点,下列结论正确的个数是( )
如图,F是△ABC的AB边上一点,下列结论正确的个数是( )①若∠AFC=∠ACB,则△ACF∽△ABC
②若∠AFC=∠B,则△ACF∽△ABC
③若AC2=AF•AB,则△ACF∽△ABC
④若AC:CF=AB:BC,则△ACF∽△ABC.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 由于两个三角形有公共角,则根据有两组角对应相等的两个三角形相似可对①进行判断,根据三角形外角性质可对②进行判断;根据两组对应边的比相等且夹角对应相等的两个三角形相似可对③④进行判断.
解答 解:∵∠FAC=∠CAB,
∴当∠AFC=∠ACB,则△ACF∽△ABC,所以①正确;
而∠AFC>∠B,所以②错误;
当AC:AB=AF:AC,即AC2=AF•AB,△ACF∽△ABC,所以③正确,④错误.
故选C.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 已知AB∥CD,直线MN分别交AB,CD于E、F,∠MFD=50°,EG平分∠MEB,求∠MEG的度数.
已知AB∥CD,直线MN分别交AB,CD于E、F,∠MFD=50°,EG平分∠MEB,求∠MEG的度数.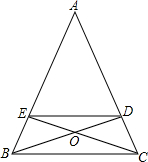 已知,如图,△ABC中,AB=AC,BD,CE为△ABC的高,且BD,CE交于点O.
已知,如图,△ABC中,AB=AC,BD,CE为△ABC的高,且BD,CE交于点O. 如图,由点A(a,0),O(0,0),B(-a,a+3)(a>0),确定的△AOB的面积为2,求a的值.
如图,由点A(a,0),O(0,0),B(-a,a+3)(a>0),确定的△AOB的面积为2,求a的值. 如图是2009年7月的台历,用“
如图是2009年7月的台历,用“ ”形框数,每次框出5个数.
”形框数,每次框出5个数.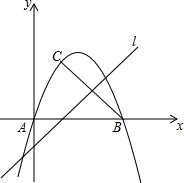 我们将使得函数值为零的自变量的值称为函数的零点值,此时的点称为函数的零点.例如,对于函数y=x-1,令y=0,可得x=1,我们就说1是函数y=x-1的零点值,点(1,0)是函数y=x-1的零点.已知二次函数y=kx2-(4k+1)x+3k+3.
我们将使得函数值为零的自变量的值称为函数的零点值,此时的点称为函数的零点.例如,对于函数y=x-1,令y=0,可得x=1,我们就说1是函数y=x-1的零点值,点(1,0)是函数y=x-1的零点.已知二次函数y=kx2-(4k+1)x+3k+3.