题目内容
12. 如图,某小区内有一块长、宽比为2:1的矩形空地,计划在该空地上修筑两条宽为2m的互相垂直的小路,余下的四块小矩形空地铺成草坪,如果四块草坪的面积之和为312m2,请求出原来大矩形空地的长和宽.
如图,某小区内有一块长、宽比为2:1的矩形空地,计划在该空地上修筑两条宽为2m的互相垂直的小路,余下的四块小矩形空地铺成草坪,如果四块草坪的面积之和为312m2,请求出原来大矩形空地的长和宽.(1)请找出上述问题中的等量关系:矩形面积减去道路面积=四块草坪的面积之和;
(2)若设大矩形空地的宽为x m,可列出的方程为x•2x-(2x+2•2x-4)=312,方程的解为x1=14,x2=-11,原来大矩形空地的长和宽分别为28m、14m.
分析 (1)根据矩形面积减去道路面积,也就是四块草坪的面积之和,可知本题的等量关系;
(2)根据(1)中的等量关系列出代数式,即可得到方程解之即可.
解答 解:(1)根据矩形面积减去道路面积,也就是四块草坪的面积之和,所以等量关系为:矩形面积减去道路面积=四块草坪的面积之和,
故答案为:矩形面积减去道路面积=四块草坪的面积之和;
(2)设矩形的宽为xm,则长为2xm,根据题意列方程,
x•2x-(2x+2•2x-4)=312
整理得:2x2-6x-308=0,
解得x1=14,x2=-11(不合题意,舍去),
2x=28,
答:原来大矩形空地的长和宽分别为28m、14m.
故答案为:x•2x-(2x+2•2x-4)=312,x1=14,x2=-11,28m、14m.
点评 本题主要考查了一元二次方程的实际应用-面积问题,利用简单组合图形的面积找到等量关系列出方程解决问题.

练习册系列答案
相关题目
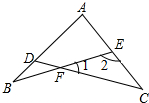 如图,∠B=25°,∠C=35°,∠A-∠1=60°,求∠A的度数.
如图,∠B=25°,∠C=35°,∠A-∠1=60°,求∠A的度数.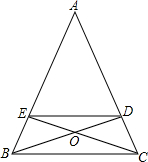 已知,如图,△ABC中,AB=AC,BD,CE为△ABC的高,且BD,CE交于点O.
已知,如图,△ABC中,AB=AC,BD,CE为△ABC的高,且BD,CE交于点O. 如图是2009年7月的台历,用“
如图是2009年7月的台历,用“ ”形框数,每次框出5个数.
”形框数,每次框出5个数.