题目内容
20．若抛物线y=x2-2x+c与y轴的交点为（0，-3），则下列说法不正确的是（ ）| A． | 抛物线开口向上 | B． | 当x=1时，y的最大值为4 | ||
| C． | 对称轴直线是x=1 | D． | 抛物线与x轴的交点为（-1，0），（3，0） |
分析 把（0，-3）代入抛物线解析式求c的值，然后再求出顶点坐标、与x轴的交点坐标．
解答 解：把（0，-3）代入y=x2-2x+c中得c=-3，
抛物线为y=x2-2x-3=（x-1）2-4=（x+1）（x-3），
所以：抛物线开口向上，对称轴是x=1，
当x=1时，y的最小值为-4，
与x轴的交点为（-1，0），（3，0）；
观察选项，B选项符合题意．
故选：B．
点评 本题考查了二次函数的性质．要求掌握抛物线的性质并对其中的a，b，c熟悉其相关运用．
练习册系列答案
相关题目
8．下列计算正确的是（ ）
| A． | $（-\frac{1}{2}）^{2}=-\frac{1}{4}$ | B． | 3a-2=$\frac{1}{3{a}^{2}}$ | C． | （-1）0=1 | D． | 00=1 |
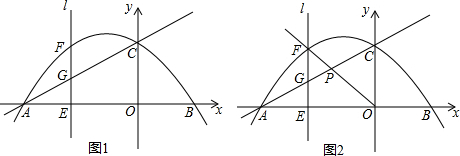
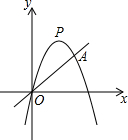如图，二次函数y=-x2+4x与一次函数y=$\frac{1}{2}$x的图象相交于点A．
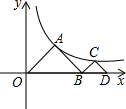如图所示，点A、C都是双曲线y=$\frac{4}{x}$在第一象限分支上的点，且△AOB和△BCD都是等腰直角三角形，∠A=∠C=90°，求点D的坐标．