题目内容
10．菱形ABCD中，AB=4cm，∠ABC=60°，则此菱形ABCD的面积为8$\sqrt{3}c{m}^{2}$．分析 根据菱形的性质以及锐角三角函数关系得出AE的长，即可得出菱形的面积．
解答 解：如图所示：过点A作AE⊥DC于点E，
∵在菱形ABCD中，AB=2，∠ABC=60°，
∴∠D=60°，AB=AD=DC=4cm，
∴AE=AD•sin60°=$2\sqrt{3}$cm，
∴菱形ABCD的面积S=AE×DC=8$\sqrt{3}$cm2．
故答案为：8$\sqrt{3}$cm2．
点评 此题主要考查了菱形的面积以及其性质，得出AE的长是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
20．为了了解某市七年级学生的体重情况，相关人员抽查了该市1000名七年级学生，则下列说法中错误的是（ ）
| A． | 该市七年级学生的全体是总体 | |
| B． | 每个七年级学生的体重是个体 | |
| C． | 抽查的1000名学生的体重是总体的一个样本 | |
| D． | 这次调查样本的容量是1000 |
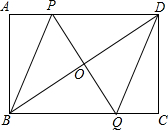如图，矩形ABCD中，点P是线段AD上的一个动点，O为BD的中点，PO的延长线交BC于Q．
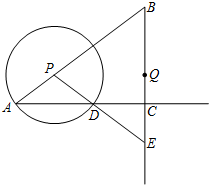如图，在Rt∠ABC中，∠ACB=90°，AC=8，tanB=$\frac{4}{3}$，点P是线段AB上的一个动点，以点P为圆心，PA为半径的⊙P与射线AC的另一个交点为点D，射线PD交射线BC于点E，点Q是线段BE的中点．
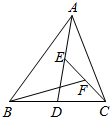如图，在△ABC中，点D、E、F分别为BC、AD、CE的中点．若S△BFC=1，则S△ABC=4．
2．下列化简正确的是（ ）
| A． | $\sqrt{\frac{2}{3}}$=$\frac{\sqrt{2}}{3}$ | B． | $\sqrt{40}$=5$\sqrt{8}$ | C． | $\sqrt{\frac{8}{9}}$=$\frac{4\sqrt{2}}{3}$ | D． | 8$\sqrt{\frac{3}{2}}$=4$\sqrt{6}$ |