题目内容
20.二次函数y=-x2+mx+n的图象经过点A(-1,4),B(1,0),$y=-\frac{1}{2}x+b$经过点B,且与二次函数y=-x2+mx+n交于点D.过点D作DC⊥x轴,垂足为点C.(1)求二次函数的表达式;
(2)点N是二次函数图象上一点(点N在BD上方),过N作NP⊥x轴,垂足为点P,交BD于点M,求MN的最大值.
分析 (1)根据待定系数法求得即可;
(2)根据待定系数法求得b,得到直线的解析式,设M(m,-$\frac{1}{2}$m+$\frac{1}{2}$),则N(m,-m2-2m+3),则MN=-m2-2m+3-(-$\frac{1}{2}$m+$\frac{1}{2}$)=-m2-$\frac{3}{2}$m+$\frac{5}{2}$=-(m+$\frac{3}{4}$)2+$\frac{49}{16}$,从而求得最大值.
解答 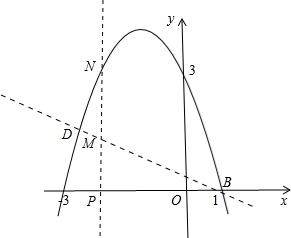 解:(1)∵二次函数y=-x2+mx+n的图象经过点A(-1,4),B(1,0)
解:(1)∵二次函数y=-x2+mx+n的图象经过点A(-1,4),B(1,0)
∴$\left\{\begin{array}{l}{4=-1-m+n}\\{0=-1+m+n}\end{array}\right.$
解得m=-2,n=3
∴二次函数的表达式为y=-x2-2x+3;
(2)$y=-\frac{1}{2}x+b$经过点B,
∴-$\frac{1}{2}$×1+b=0,
∴解得b=$\frac{1}{2}$
∴y=-$\frac{1}{2}$x+$\frac{1}{2}$
设M(m,-$\frac{1}{2}$m+$\frac{1}{2}$),则N(m,-m2-2m+3),
∴MN=-m2-2m+3-(-$\frac{1}{2}$m+$\frac{1}{2}$)=-m2-$\frac{3}{2}$m+$\frac{5}{2}$=-(m+$\frac{3}{4}$)2+$\frac{49}{16}$,
∴MN的最大值为$\frac{49}{16}$.
点评 本题考查了待定系数法求一次函数和二次函数的解析式,以及二次函数的最值,根据一次函数和二次函数表示出M、N的坐标是解题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
8.某校学生参加体育测试,某小组10名同学的完成引体向上的个数如下表,
这10名同学引体向上个数的众数与中位数依次是( )
| 完成引体向上的个数 | 10 | 9 | 8 | 7 |
| 人 数 | 1 | 1 | 3 | 5 |
| A. | 7和7.5 | B. | 7和8 | C. | 7.5和9 | D. | 8和9 |
5.直角三角形的两直角边均扩大到原来的两倍,则斜边扩大到原来的( )
| A. | 8倍 | B. | 4倍 | C. | 2倍 | D. | 6倍 |
10.北京的水资源非常匮乏,为促进市民节水,从2014年5月1日起北京市居民用水实行阶梯水价,实施细则如表:
北京市居民用水阶梯水价表 单位:元/立方米
某户居民从2015年1月1日至4月30日,累积用水190立方米,则这户居民4个月共需缴纳水费970元.
北京市居民用水阶梯水价表 单位:元/立方米
| 分档水量 | 户年用水量 (立方米) | 水价 | 其中 | ||
| 自来水费 | 水资源费 | 污水 处理费 | |||
| 第一阶梯 | 0-180(含) | 5.00 | 2.07 | 1.57 | 1.36 |
| 第二阶梯 | 181-260(含) | 7.00 | 4.07 | ||
| 第三阶梯 | 260以上 | 9.00 | 6.07 | ||
 已知△ABC,如图所示
已知△ABC,如图所示