题目内容
18.△ABC中,AB=8,BC=6,AC=4,点M在CA的延长线上,点N在BA的延长线上,若ABC与MAN相似,且MN=3,则CM的长为6或8.分析 分类讨论:当△ABC∽△ANM时,根据相似三角形的性质得$\frac{AM}{4}$=$\frac{3}{6}$,当△ABC∽△AMN时,根据相似三角形的性质得$\frac{AM}{8}$=$\frac{3}{6}$,然后利用比例性质分别求出AM,然后得到对应的CM的长.
解答 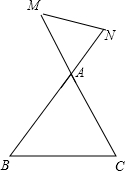 解:如图,
解:如图,
当△ABC∽△ANM时,$\frac{AM}{AC}$=$\frac{MN}{BC}$,即$\frac{AM}{4}$=$\frac{3}{6}$,解得AM=2,所以CM=AM+AC=2+4=6;
当△ABC∽△AMN时,$\frac{AM}{AB}$=$\frac{MN}{BC}$,即$\frac{AM}{8}$=$\frac{3}{6}$,解得AM=4,所以CM=AM+AC=4+4=8,
综上所述,CM的长为6或8.
故答案为6或8.
点评 本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等;相似三角形(多边形)的周长的比等于相似比;相似三角形的对应线段(对应中线、对应角平分线、对应边上的高)的比也等于相似比;相似三角形的面积的比等于相似比的平方.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.在Rt△ABC中,∠C=90°,若AC=4,AB=5,则cosB的值( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
10.下列命题正确的为( )
| A. | 平分弦的直径垂直于弦 | |
| B. | 过三点可以作圆 | |
| C. | 在同圆或等圆中,等弦所对的圆周角相等 | |
| D. | 三角形的外心到三角形的三个顶点的距离相等 |
 在△ABC中,∠C=90°,△ABC的面积为6,斜边长为6,则tanA+tanB的值为3.
在△ABC中,∠C=90°,△ABC的面积为6,斜边长为6,则tanA+tanB的值为3.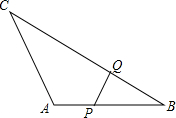 如图,在△ABC中,AB=8,BC=16,点P从点A开始沿AB向点B以2m/s的速度移动,点Q从点B开始沿BC向点C以4m/s的速度移动,如果P,Q分别从AB,BC同时出发,经过几秒△PBQ与△ABC相似?
如图,在△ABC中,AB=8,BC=16,点P从点A开始沿AB向点B以2m/s的速度移动,点Q从点B开始沿BC向点C以4m/s的速度移动,如果P,Q分别从AB,BC同时出发,经过几秒△PBQ与△ABC相似?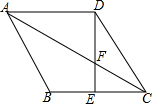 如图,菱形ABCD中,E为BC中点,DE与对角线AC交于点F,CF=DF.
如图,菱形ABCD中,E为BC中点,DE与对角线AC交于点F,CF=DF.