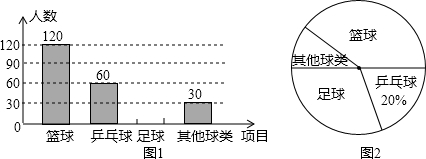
题目内容
7.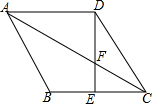 如图,菱形ABCD中,E为BC中点,DE与对角线AC交于点F,CF=DF.
如图,菱形ABCD中,E为BC中点,DE与对角线AC交于点F,CF=DF.(1)求证:DE⊥BC;
(2)若CE=1,求菱形ABCD的面积.
分析 (1)首先过点F作FM⊥CD于点M,由CF=DF,可得M是CD的中点,又由菱形ABCD中,E为BC中点,利用SAS可判定△CFM≌△CFE,即可证得DE⊥BC;
(2)由CE=1,可求得BC=CD=2,然后由勾股定理求得DE的长,继而求得菱形ABCD的面积.
解答 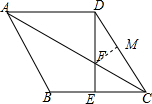 (1)证明:过点F作FM⊥CD于点M,
(1)证明:过点F作FM⊥CD于点M,
∵CF=DF,
∴CM=$\frac{1}{2}$CD,
∵四边形ABCD是菱形,
∴∠MCF=∠ECF,BC=CD,
∵E为BC中点,
∴CE=CM,
在△CFM和△CFE中,
$\left\{\begin{array}{l}{CE=CM}\\{∠ECF=∠MCF}\\{CF=CF}\end{array}\right.$,
∴△CFM≌△CFE(SAS),
∴∠CEF=∠CMF=90°,
即DE⊥BC;
(2)解:∵CE=1,
∴BC=CD=2CE=2,
∵DE⊥BC,
∴DE=$\sqrt{C{D}^{2}-C{E}^{2}}$=$\sqrt{3}$,
∴S菱形ABCD=BC•DE=2$\sqrt{3}$.
点评 此题考查了菱形的性质、全等三角形的判定与性质以及勾股定理.注意辅助线的构造是关键.

练习册系列答案
相关题目
 如图,在△ABC中DE∥C,交AB,AC于点D,E,试证明$\frac{AD}{AB}=\frac{DO}{CO}$.
如图,在△ABC中DE∥C,交AB,AC于点D,E,试证明$\frac{AD}{AB}=\frac{DO}{CO}$.