题目内容
8.设m、n是一元二次方程x2+2x-5=0的两个根,则m2+3m+n=3.分析 先根据一元二次方程的解的定义得到m2+2m-5=0,则m2=-2m+5,代入m2+3m+n得到m+n+5,然后根据根与系数的关系得到m+n=-2,再利用整体代入的方法计算.
解答 解:∵m是一元二次方程x2+2x-5=0的根,
∴m2+2m-5=0,即m2=-2m+5,
∴m2+3m+n=-2m+5+3m+n
=m+n+5,
∵m、n为方程x2+2x-5=0的两个根,
∴m+n=-2,
∴m2+3m+n=-2+5=3.
故答案为:3.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.也考查了一元二次方程的解.

练习册系列答案
相关题目
19.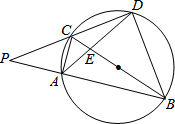 如图所示,BC为圆的直径,图中相似三角形的对数共有( )
如图所示,BC为圆的直径,图中相似三角形的对数共有( )
 如图所示,BC为圆的直径,图中相似三角形的对数共有( )
如图所示,BC为圆的直径,图中相似三角形的对数共有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
13.已知⊙O1的半径是5cm,⊙O2的半径是3cm,O1O2=6cm,则⊙O1和⊙O2的位置关系是( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内含 |
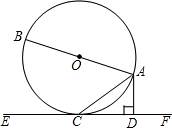 如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC. 如图,DE是△ABC的中位线,DE=2cm,AB+AC=12cm,则△ABC的周长是16cm.
如图,DE是△ABC的中位线,DE=2cm,AB+AC=12cm,则△ABC的周长是16cm. 将形状相同.大小相等的两个长方体小木块按如图所示放置在水平面上,则其主视图是( )
将形状相同.大小相等的两个长方体小木块按如图所示放置在水平面上,则其主视图是( )


