题目内容
9.解不等式:y+$\frac{y-1}{2}$≤$\frac{y-2}{3}$,并把解集表示在数轴上.分析 根据解一元一次不等式的步骤,求出不等式的解集,并把解集在数轴上表示出来即可.
解答 解;y+$\frac{y-1}{2}$≤$\frac{y-2}{3}$,
去分母得:6y+3(y-1)≤2(y-2),
去括号得:6y+3y-3≤2y-4
移项得:6y+3y-2y≤3-4
合并同类项得:7y≤-1
系数化1得:y≤-$\frac{1}{7}$.
在数轴上表示为: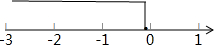
点评 此题考查了一元一次不等式,要掌握解一元一次不等式的步骤,会解集在数轴上表示出来,注意x$≤-\frac{1}{7}$要用实心的圆点.

练习册系列答案
相关题目
1.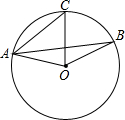 如图,在⊙O中,∠BAC=25°,则∠BOC的度数为( )
如图,在⊙O中,∠BAC=25°,则∠BOC的度数为( )
 如图,在⊙O中,∠BAC=25°,则∠BOC的度数为( )
如图,在⊙O中,∠BAC=25°,则∠BOC的度数为( )| A. | 25° | B. | 50° | C. | 60° | D. | 80° |
18.方程x2-4x+4=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有一个实数根 | D. | 没有实数根 |
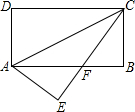 如图.在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点E处,且CE与AB交于F,那么S△ACF为( )
如图.在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点E处,且CE与AB交于F,那么S△ACF为( )