题目内容
关于x的一元二次方程(a-1)x2-2x+1=0有实数根,则a的取值范围是 .
考点:根的判别式,一元二次方程的定义
专题:
分析:根据根的判别式和一元二次方程的定义可得△=b2-4ac≥0,且a-1≠0,再进行整理即可.
解答:解:∵一元二次方程(a-1)x2-2x+1=0有实数根,
∴△=b2-4ac=(-2)2-4(a-1)≥0,且a-1≠0,
∴a≤2且a≠1.
故答案为:a≤2且a≠1.
∴△=b2-4ac=(-2)2-4(a-1)≥0,且a-1≠0,
∴a≤2且a≠1.
故答案为:a≤2且a≠1.
点评:此题考查了根的判别式和一元二次方程的定义,根的判别式大于0,方程有两个不相等的实数根;根的判别式等于0,方程有两个相等的实数根;根的判别式小于0,方程没有实数根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知线段m、n(m>n),用直尺和圆规作等腰△ABC,使AB=AC=m,BC=n,再分别以AB、AC为边向形外作等边△ABD和等边△ACE,连接BE、CD,则( )
| A、BE>CD |
| B、BE=CD |
| C、BE<CD |
| D、BE≤CD |
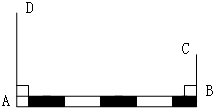 如图,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=24千米,BC=16千米,求两个村庄的距离.
如图,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=24千米,BC=16千米,求两个村庄的距离.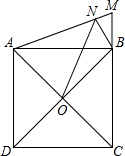 如图,正方形ABCD的边长为3,延长CB到点M,使BM=1,连接AM,过点B作BN⊥AM,垂足为N,O是对角线AC、BD的交点,连接ON,则ON的长为
如图,正方形ABCD的边长为3,延长CB到点M,使BM=1,连接AM,过点B作BN⊥AM,垂足为N,O是对角线AC、BD的交点,连接ON,则ON的长为