题目内容
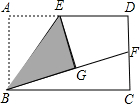（1）操作发现：如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE．且点G在矩形ABCD内部．小明将BG延长交DC于点F，认为GF=DF，你同意吗？请说明理由．（2）问题解决：保持（1）中的条件不变，若DF=4，CD=9，求
| AD |
| AB |
（3）推广延伸：保持（1）中的条件不变，若DC=2DF，求
| AD |
| AB |
考点：翻折变换（折叠问题）
专题：
分析：（1）求简单的线段相等，可证线段所在的三角形全等，即连接EF，证△EGF≌△EDF即可；
（2）分别求出BF、CF，在RT△BCF中，利用勾股定理即可得出答案；
（3）可设DF=x，BC=y；进而可用x表示出DC、AB的长，根据折叠的性质知AB=BG，即可得到BG的表达式，由（1）证得GF=DF，那么GF=x，由此可求出BF的表达式，进而可在Rt△BFC中，根据勾股定理求出x、y的比例关系，即可得到
的值．
（2）分别求出BF、CF，在RT△BCF中，利用勾股定理即可得出答案；
（3）可设DF=x，BC=y；进而可用x表示出DC、AB的长，根据折叠的性质知AB=BG，即可得到BG的表达式，由（1）证得GF=DF，那么GF=x，由此可求出BF的表达式，进而可在Rt△BFC中，根据勾股定理求出x、y的比例关系，即可得到
| AD |
| AB |
解答：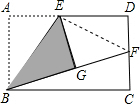
解：（1）同意．连接EF，
则∠EGF=∠D=90°，EG=AE=ED，EF=EF，
∴Rt△EGF≌Rt△EDF．
∴GF=DF．
（2）由题意得，CF=CD-DF=5，BF=BG+GF=AB+DF=13，设AD=x，则BC=x，
在Rt△BCF中，BC2+CF2=BF2，即x2+25=169，
解得：x=12，即AD=12．
=
=
．
故
的值为
；
（3）由（1）知，GF=DF．
设DF=x，BC=y，
则有GF=x，AD=y．
∵DC=2DF，
∴CF=x，DC=AB=BG=2x，
∴BF=BG+GF=3x．
在Rt△BCF中，BC2+CF2=BF2．即y2+x2=（3x）2．
∴y=2
x，
∴
的=
=
．
解：（1）同意．连接EF，则∠EGF=∠D=90°，EG=AE=ED，EF=EF，
∴Rt△EGF≌Rt△EDF．
∴GF=DF．
（2）由题意得，CF=CD-DF=5，BF=BG+GF=AB+DF=13，设AD=x，则BC=x，
在Rt△BCF中，BC2+CF2=BF2，即x2+25=169，
解得：x=12，即AD=12．
| AD |
| AB |
| 12 |
| 9 |
| 4 |
| 3 |
故
| AD |
| AB |
| 4 |
| 3 |
（3）由（1）知，GF=DF．
设DF=x，BC=y，
则有GF=x，AD=y．
∵DC=2DF，
∴CF=x，DC=AB=BG=2x，
∴BF=BG+GF=3x．
在Rt△BCF中，BC2+CF2=BF2．即y2+x2=（3x）2．
∴y=2
| 2 |
∴
| AD |
| AB |
| y |
| 2x |
| 2 |
点评：此题考查了矩形的性质、图形的折叠变换、全等三角形的判定和性质、勾股定理的应用等重要知识，难度适中．
练习册系列答案
相关题目
下列说法不正确的是（ ）
| A、没有最大的实数，也没有最小的实数 | ||
B、
| ||
C、如果
| ||
| D、两个无理数的和有可能是有理数 |
如图：已知：AB=AC，AD=AE．求证：BO=CO．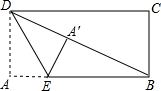
如图，在矩形纸片ABCD中，AB=12，BC=5，点E在AB上，将△DAE沿DE折叠，使点A落在对角线BD上的点A′处，求AE的长为多少？