题目内容
16．已知一次函数y=kx+b的图象经过点（-2，5），并且与y轴交于点P，直线y=$\frac{1}{2}$x+3与y轴交于点Q，点Q恰与点P关于x轴对称，求这个一次函数的解析式．分析 因为直线y=$\frac{1}{2}$x+3与y轴相交于点Q，所以点Q的坐标是（0，3），点P在y轴上，且与点P关于x轴对称，所以点P的坐标是（0，-3），把（0，-3），（-2，5）代入一次函数y=kx+b．求出k，b的值，得这个一次函数的表达式．
解答 解：由题意可得，点Q的坐标是（0，3），点P的坐标是（0，-3），
把（0，-3），（-2，5）代入一次函数y=kx+b得$\left\{\begin{array}{l}{b=-3}\\{-2k+b=5}\end{array}\right.$，
解得b=-3，k=-4．
所以这个一次函数的表达式：y=-4x-3．
点评 本题考查了待定系数法求一次函数解析式，一次函数图象上点的坐标特征，关于x轴、y轴对称的点的坐标坐标，正确的理解题意是解题的关键．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
如图是一大一小的两个可以自由转动的转盘，甲盘被平均分成6等份，乙盘被平均分成4等份，每个转盘均被涂上红、黄、蓝三种颜色，转动转盘，当转盘停止后，指针指向的颜色即为转出的颜色，小明与小颖参与游戏；小明转动甲盘，小颖转动乙盘．
小颖站在自家阳台的A处用测角仪观察对面的商场，如图，在A处测得商场楼顶B点的俯角为45°，商场楼底C点的俯角为60°，若商场高17.6米，小颖家所在楼房每层楼的平均高度为3米，则小颖家住在几楼？小颖家与商场相距多少米？（结果保留整数，参考数据：$\sqrt{3}$≈1.732，$\sqrt{2}$≈1.414）
11．为了分析学生数学竞赛成绩，指导老师对全体参赛选手的竞赛成绩进行统计，结果如下（单位；分）；
91 68 73 90 87 71 61 75 82 77 80 82 93 85 76
78 87 74 88 65 72 86 71 69 72 79 81 90 66 70
75 82 77 78 75 85 72 95 80 79 77 78 83 80 83
（1）填写下面的频数分布表．
当分数在60～74时，成绩为及格；当分数在75～84时，成绩为良好；当分数在85～100时，成绩为优秀，请用扇形图表示出及格、良好、优秀所占的百分比．
91 68 73 90 87 71 61 75 82 77 80 82 93 85 76
78 87 74 88 65 72 86 71 69 72 79 81 90 66 70
75 82 77 78 75 85 72 95 80 79 77 78 83 80 83
（1）填写下面的频数分布表．
| 分组 | 划记 | 频数 |
| 60.5～65.5 |  | 2 |
| 65.5～70.5 | 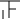 | 4 |
| 70.5～75.5 | 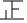 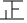 | 10 |
| 75.5～80.5 | 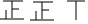 | 12 |
| 80.5～85.5 |  | 8 |
| 85.5～90.5 |  | 6 |
| 90.5～95.5 | 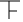 | 3 |
| 合计 |
8．
某批发部队外批发一种小商品，每个售价m元，如果一次购买100分以上，超过100个的部分售价打8折，付款金额y（元）与购买数量x（个）之间的关系如图所示，该批发部老板将某一天的销售情况绘制成如图所示的表格．
（1）求出y与x之间的函数表达式；
（2）m=5，a=300，b=900，c=350．
（3）若该小商品的进价为2元/个，请求出该批发部这一天所获得的利润．
某批发部队外批发一种小商品，每个售价m元，如果一次购买100分以上，超过100个的部分售价打8折，付款金额y（元）与购买数量x（个）之间的关系如图所示，该批发部老板将某一天的销售情况绘制成如图所示的表格．| 购买数量x（个） | 60 | 100 | 120 | 200 | c |
| 付款金额y（元） | a | 500 | 580 | b | 1500 |
（2）m=5，a=300，b=900，c=350．
（3）若该小商品的进价为2元/个，请求出该批发部这一天所获得的利润．