题目内容
 如图,正方形ABCD的两条对角线相交于点O,点M,N分别在OA,OD上,且MN∥AD,请探究线段DM和CN之间的数量关系,写出结论并给出证明.
如图,正方形ABCD的两条对角线相交于点O,点M,N分别在OA,OD上,且MN∥AD,请探究线段DM和CN之间的数量关系,写出结论并给出证明.考点:全等三角形的判定与性质,正方形的性质
专题:证明题
分析:由四边形ABCD为正方形,利用正方形的对角线互相平分、相等且垂直,得到OA=OB=OC=OD,且∠DOM=∠CON=90°,根据MN与AD平行,得到三角形OMN与三角形OAD相似,由相似得比例得到OM=ON,利用SAS得到三角形DOM与三角形CON全等,利用全等三角形对应边相等即可得证.
解答:答:DM=CN,理由为:
证明:∵四边形ABCD为正方形,
∴OA=OB=OC=OD,
∠DOM=∠CON=90°,
∵MN∥AD,
∴△OMN∽△OAD,
∴
=
,即OM=ON,
在△DOM和△CON中,
,
∴△DOM≌△CON(SAS),
∴DM=CN.
证明:∵四边形ABCD为正方形,
∴OA=OB=OC=OD,
∠DOM=∠CON=90°,
∵MN∥AD,
∴△OMN∽△OAD,
∴
| OM |
| OA |
| ON |
| OD |
在△DOM和△CON中,
|
∴△DOM≌△CON(SAS),
∴DM=CN.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
甲、乙两人在相同的条件下,各射靶10次,经过计算:甲、乙的平均数均是7,甲的方差是1.2,乙的方差是1.8,则下列说法中不正确的是( )
| A、甲、乙射中的总环数相同 |
| B、甲的成绩稳定 |
| C、乙的成绩波动较大 |
| D、甲、乙的众数相同 |
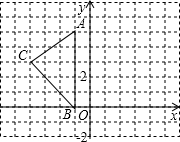 如图,在平面直角坐标系中,已知A(-1,5),B(-1,0),C(-4,3).
如图,在平面直角坐标系中,已知A(-1,5),B(-1,0),C(-4,3). 如图,菱形ABCD的对角线AC与BD相交于点O,过点O的直线EF分别与边AD、相交于点E和F,∠ABC与∠BAD的度数比为1:2,菱形ABCD的周长为32cm.
如图,菱形ABCD的对角线AC与BD相交于点O,过点O的直线EF分别与边AD、相交于点E和F,∠ABC与∠BAD的度数比为1:2,菱形ABCD的周长为32cm. 如图,AD∥BC,∠A=∠C,BE、DF分别平分∠ABC和∠CDA.求证:BE∥DF.
如图,AD∥BC,∠A=∠C,BE、DF分别平分∠ABC和∠CDA.求证:BE∥DF. 如图,先将正方形纸片ABCD对折,折痕为EF,再把点C折叠在EF上,折痕为DG,点C在 EF上对应点为P,则∠CPE=
如图,先将正方形纸片ABCD对折,折痕为EF,再把点C折叠在EF上,折痕为DG,点C在 EF上对应点为P,则∠CPE=