题目内容
15.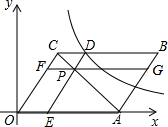 如图,在平面直角坐标系中,O为坐标原点,?OABC的边OA落在x轴正半轴上,顶点C(3,4),点P为对角线AC上一点,过点P分别作DE∥OC,FG∥OA分别交?OABC各边如图所示,反比例函数y=$\frac{k}{x}$图象过点D.
如图,在平面直角坐标系中,O为坐标原点,?OABC的边OA落在x轴正半轴上,顶点C(3,4),点P为对角线AC上一点,过点P分别作DE∥OC,FG∥OA分别交?OABC各边如图所示,反比例函数y=$\frac{k}{x}$图象过点D.(1)若四边形DCOE的面积为4,求k的值;
(2)若四边形PDCF是菱形,求点B的坐标.
分析 (1)过C作CM⊥x轴于点M,由平行四边形DCOE的面积可求得OE,过D作DN⊥x轴于点N,由C点坐标则可求得ON的长,从而可求得D点坐标,代入反比例函数解析式可求得k的值;
(2)延长BC交y轴于点Q,由四边形PDCF为菱形可证得四边形OABC为菱形,由C点坐标可求得OC的长,从而可求得OQ和BQ的长,可求得B点坐标.
解答 解:
(1)如图1,过C作CM⊥x轴于点M,过D作DN⊥x轴于点N,则四边形CMND为矩形,
∵四边形OABC为平行四边形,
∴CD∥OE,且DE∥OC,
∴四边形DCOE为平行四边形,
∵C(3,4),
∴OM=3,CM=4,
∴S四边形DCOE=OE•CM=4,即4OE=4,解得OE=1,
∴CD=MN=1,
∴ON=OM+MN=3+1=4,DN=CM=4,
∴D(4,4),
∵反比例函数y=$\frac{k}{x}$图象过点D,
∴k=4×4=16;
(2)如图2,过延长BC交y轴于点Q,
∵BC∥OA,
∴BQ⊥y轴,
∵C(3,4),
∴OQ=4,CQ=3,
在Rt△OCQ中,由勾股定理可求得OC=5,
当四边形PDCF为菱形时,则∠OCA=∠BCA=∠BAC,
∴BA=BC,且四边形OABC为平行四边形,
∴四边形OABC为菱形,
∴BC=OC=5,
∴BQ=CQ+BC=3+5=8,
∴B(8,4).
点评 本题为反比例函数的综合应用,涉及待定系数法、平行四边形的性质、勾股定理、菱形的性质等知识.在(1)中求得D点坐标是解题的关键,在(2)由条件证得四边形OABC为菱形是解题的关键.本题考查知识点较多,综合性较强,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

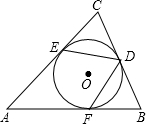 如图,已知⊙O内切于△ABC,切点分别为D、E、F,若∠A=50°,则∠EDF=65°.
如图,已知⊙O内切于△ABC,切点分别为D、E、F,若∠A=50°,则∠EDF=65°. 如图,四边形ABCD的顶点均在⊙O上,⊙O的半径为2,如果∠D=45°,那么$\widehat{AC}$的长为π(结果用π表示).
如图,四边形ABCD的顶点均在⊙O上,⊙O的半径为2,如果∠D=45°,那么$\widehat{AC}$的长为π(结果用π表示). 已知在平面直角坐标系中,已知A(2,3),B(3,5),点P为直线y=x-2上一个动点,当|PB-PA|值最大时,点P的坐标为(-1,-3).
已知在平面直角坐标系中,已知A(2,3),B(3,5),点P为直线y=x-2上一个动点,当|PB-PA|值最大时,点P的坐标为(-1,-3).
