题目内容
10.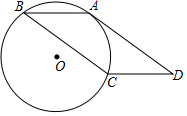 如图,?ABCD的边AD与经过A,B,C三点的⊙O相切,sin∠D=$\frac{5}{13}$,AD=24,则⊙O的半径为$\frac{169}{10}$.
如图,?ABCD的边AD与经过A,B,C三点的⊙O相切,sin∠D=$\frac{5}{13}$,AD=24,则⊙O的半径为$\frac{169}{10}$.
分析 如图连接OB、OA,OA交BC于E,首先证明OA⊥BC,推出BE=EC=12,在Rt△ABE中,求出AB、AE,再在Rt△BOE中,求出OB即可.
解答 解:如图连接OB、OA,OA交BC于E.
∵四边形ABCD是平行四边形,
∴∠D=∠ABC,AD∥BC,AD=BC=24,
∵AD是⊙O的切线,
∴AD⊥OA,
∴OA⊥BC,
∴BE=EC=12,
在Rt△ABE中,sin∠ABE=sin∠D=$\frac{5}{13}$=$\frac{AE}{AB}$,
∵BE=13,
∴AE=5,AB=13,设半径为x,
在Rt△OBE中,∵OB2=BE2+OE2,
∴x2=122+(x-5)2,
∴x=$\frac{169}{10}$,
∴⊙O是半径为$\frac{169}{10}$,
故答案为$\frac{169}{10}$.
点评 本题考查切线的性质、平行四边形的性质、解直角三角形等知识,解题的关键是学会添加常用辅助线,属于中考常考题型.

练习册系列答案
相关题目
18. 已知一次函数y=kx+b的图象如图所示,则不等式kx+b>-1的解集是( )
已知一次函数y=kx+b的图象如图所示,则不等式kx+b>-1的解集是( )
 已知一次函数y=kx+b的图象如图所示,则不等式kx+b>-1的解集是( )
已知一次函数y=kx+b的图象如图所示,则不等式kx+b>-1的解集是( )| A. | x>-2 | B. | x<-2 | C. | x>0 | D. | x<0 |
2.小杨和小姜住在同一个小区,该小区到苏果超市有A、B、C三条路线
(1)求小杨随机选择一条路线,恰好是A路线的概率;
(2)求小杨和小姜两人分别随机选择一条路线去苏果超市,恰好两人选择同一条路线的概率.
(1)求小杨随机选择一条路线,恰好是A路线的概率;
(2)求小杨和小姜两人分别随机选择一条路线去苏果超市,恰好两人选择同一条路线的概率.
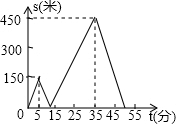 甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数函数图象的一部分如图所示.当甲乙两人相距360米时,求所有符合条件的t的值的和为68.5.
甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数函数图象的一部分如图所示.当甲乙两人相距360米时,求所有符合条件的t的值的和为68.5.
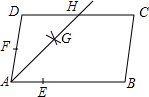 如图,在?ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F,再分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )
如图,在?ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F,再分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )