题目内容
7.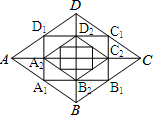 如图,菱形ABCD的对角线长分别为a、b,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,…,如此下去,得到四边形A2016B2016C2016D2016的面积用含a,b的代数式表示为($\frac{1}{2}$)2017ab.
如图,菱形ABCD的对角线长分别为a、b,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,…,如此下去,得到四边形A2016B2016C2016D2016的面积用含a,b的代数式表示为($\frac{1}{2}$)2017ab.
分析 根据三角形中位线定理,逐步推理出各小长方形的面积,总结出规律,用规律解答即可.
解答 解:∵四边形ABCD中,AC=a,BD=b,且AC丄BD,
∴S四边形ABCD=$\frac{1}{2}$ab;
由三角形的中位线的性质可以推知,每得到一次四边形,它的面积变为原来的一半,
∴四边形A2016B2016C2016D2016的面积为($(\frac{1}{2})^{2017}$ab.
故答案为:$(\frac{1}{2})^{2017}$ab.
点评 本题考查的是菱形的性质及三角形中位线定理的理解及运用,灵活运用定理,注意数形结合思想的应用是解题的关键.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
18.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
15.下列事件是必然事件的是( )
| A. | 在装有5个红球的袋中摸出1个球,是红球 | |
| B. | 小麦的亩产量一定为1500千克 | |
| C. | 打开电视机,正在转播足球比赛 | |
| D. | 农历十五的晚上一定能看到圆月 |
2.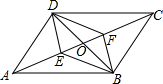 如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
 如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )| A. | ∠ADE=∠CBF | B. | ∠ABE=∠CDF | C. | DE=BF | D. | OE=OF |
16.下列各式中,能用平方差公式进行计算的是( )
| A. | (-x-y)(x+y) | B. | (2x-y)(y-2x) | C. | (1-$\frac{1}{2}$x)(-1-$\frac{1}{2}$x) | D. | (3x+y)(x-3y) |
 如图,已知AE∥BD,∠1=130°,∠2=30°,求∠C的度数.
如图,已知AE∥BD,∠1=130°,∠2=30°,求∠C的度数. 如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24 m,OE⊥CD于点E.已测得sin∠DOE=$\frac{12}{13}$.
如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24 m,OE⊥CD于点E.已测得sin∠DOE=$\frac{12}{13}$.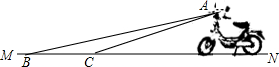 齐河路路通电动车厂新开发的一种电动车如图,它的大灯A射出的光线AB,AC 与地面MN 所夹的锐角分别为8°和10°,大灯A与地面的距离为1m则该车大灯照亮地面的宽度BC是1.4m.(不考虑其它因素)
齐河路路通电动车厂新开发的一种电动车如图,它的大灯A射出的光线AB,AC 与地面MN 所夹的锐角分别为8°和10°,大灯A与地面的距离为1m则该车大灯照亮地面的宽度BC是1.4m.(不考虑其它因素)