题目内容
13.?ABCD的对角线AC,BD相交于点O,△OAB是等边三角形,且AB=4.求?ABCD的面积.分析 由△AOB是等边三角形可以推出?ABCD是矩形,得出AC=BD=8,∠BAD=90°,由勾股定理求出AD,即可得出?ABCD的面积.
解答 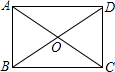 解:如图,∵?ABCD的对角线相交于点O,△AOB是等边三角形,
解:如图,∵?ABCD的对角线相交于点O,△AOB是等边三角形,
∴OA=OC,OB=OD,OA=OB=AB=4,
∴AC=BD,
∴?ABCD是矩形,
∴∠BAD=90°,AC=BD=2OA=8,
∴AD=$\sqrt{B{D}^{2}-A{B}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∴?ABCD的面积=AB•AD=4×4$\sqrt{3}$=16$\sqrt{3}$.
点评 本题主要考查了平行四边形的性质、等边三角形的性质、矩形的判定与性质、勾股定理;熟练掌握平行四边形的性质,证明四边形是矩形是解决问题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
4.下列方程①x2-2x-1=0;②ax2+bx+c=0;③$\frac{1}{{x}^{2}}$+3x-5=0;④-x2=0;⑤(x-1)2+y2=2;⑥(x-1)(x-3)=x2,其中一元二次方程共有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.有理数a等于它的倒数,有理数b等于它的相反数,则a2003+b2003的值是( )
| A. | -1 | B. | 1 | C. | 0 | D. | ±1 |
18.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5.在下列表述中,能确定位置的是( )
| A. | 北偏东30° | B. | 距学校500m的某建筑 | ||
| C. | 东经92°,北纬45° | D. | 某电影院3排 |
2.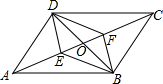 如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
 如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )| A. | ∠ADE=∠CBF | B. | ∠ABE=∠CDF | C. | DE=BF | D. | OE=OF |
3.下列运算正确的是( )
| A. | a3+a3=a6 | B. | (ab)2=a2b2 | C. | 2(a+1)=2a+1 | D. | a6÷a3=a2 |
 在Rt△EDF中,ED+DF=10,ED=EG,FD=FH.求△HDG外接圆的半径的最大值.
在Rt△EDF中,ED+DF=10,ED=EG,FD=FH.求△HDG外接圆的半径的最大值.