题目内容
10.根据要求,解答下列问题.(1)解方程组:$\left\{\begin{array}{l}{3x+2y=10}\\{2x+3y=10}\end{array}\right.$
(2)解下列方程组,只写出最后结果即可:
①$\left\{\begin{array}{l}{x+2y=3}\\{2x+y=3}\end{array}\right.$$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$;②$\left\{\begin{array}{l}{2x-y=4}\\{-x+2y=4}\end{array}\right.$$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$.
(3)以上每个方程组的解中,x值与y值有怎样的大小关系?x=y
(4)请你构造一个具有以上外形特征的方程组,并直接写出它的解.
分析 (1)用加减消元法消去x,求出y,再求出x即可、
(2)两个方程组都是用加减消元法消去x,求出y,再求出x即可、
(3)观察方程组的解即可对称结论.
(4)模仿方程组的特征构造方程组即可.
解答 解:(1)$\left\{\begin{array}{l}{3x+2y=10}&{①}\\{2x+3y=10}&{②}\end{array}\right.$
①×2-②×3得到:y=2,
代入①得x=2,
则$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$
(2)①$\left\{\begin{array}{l}{x+2y=3}&{①}\\{2x+y=3}&{②}\end{array}\right.$
①×2-②得到y=1,
代入①得x=1,
则$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$
故答案为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
②$\left\{\begin{array}{l}{2x-y=4}&{①}\\{-x+2y=4}&{②}\end{array}\right.$
①+②×2得到y=4,
代入②得x=4,
则$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$,
故答案为$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$.
(3)观察方程组的解可知x=y,
故答案为x=y.
(4)答案不唯一.$\left\{\begin{array}{l}{3x+4y=7}\\{4x+3y=7}\end{array}\right.$解为$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$.
点评 本题考查方程组的解,熟练掌握解方程组是解决问题的关键,解方程组的思想是化二元方程为一元方程,可以用代入消元,也可以用加减消元,属于中考常考题型.

| A. | -1 | B. | 1 | C. | 0 | D. | ±1 |
| A. |  | B. |  | C. |  | D. |  |
| A. | 北偏东30° | B. | 距学校500m的某建筑 | ||
| C. | 东经92°,北纬45° | D. | 某电影院3排 |
| A. | 在装有5个红球的袋中摸出1个球,是红球 | |
| B. | 小麦的亩产量一定为1500千克 | |
| C. | 打开电视机,正在转播足球比赛 | |
| D. | 农历十五的晚上一定能看到圆月 |
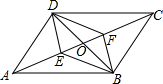 如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
如图,平行四边形ABCD中,对角线AC、BD相交于点O,E、F是AC上的两点,当E、F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )| A. | ∠ADE=∠CBF | B. | ∠ABE=∠CDF | C. | DE=BF | D. | OE=OF |