题目内容
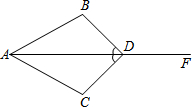 如图所示,∠ADB=∠ADC,
如图所示,∠ADB=∠ADC,(1)求证:请你添加一个条件使△ABD≌△ACD并说明理由;添加
(2)若∠B=∠C=90°,AB=8cm,BD=6cm,E从D点出发沿射线DF运动,当点E移动多少厘米时,四边形ACEB为菱形?说明你的理由.
考点:菱形的判定,全等三角形的判定与性质
专题:
分析:(1)根据题意可得:AD=AD,再有条件∠ADB=∠ADC,可添加BD=CD或∠B=∠C或∠BAD=∠ADC,可判断△ADB≌△ACD.
(2)利用菱形的性质得到AO=BO,然后求得点E的运动时间即可得到正确的答案.
(2)利用菱形的性质得到AO=BO,然后求得点E的运动时间即可得到正确的答案.
解答:解:(1)添加BD=CD或∠B=∠C或∠BAD=∠ADC,
理由:添加BD=CD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS).
(2)当E点移动2.8厘米时,四边形ACEB为菱形.
理由如下:连BC交AD于O.
∵△ABD≌△ACD(已证)
∴AB=AC,∠BAD=∠ADC
∴AO⊥BO,BO=CO
∵∠B=∠C=90°,AB=8cm,BD=6cm
∴由勾股定理可得AD=10
∵由S△ABD=
AB•BD=
AD•BO
∴BO=4.8
∴由勾股定理可得AO=6.4
∴OD=3.6
∵DE=2.8
∴OD=6.4
∴AO=OD
∴四边形ACEB为菱形(对角线互相垂直平分的四边形为菱形).
理由:添加BD=CD,
在△ABD和△ACD中,
|
∴△ABD≌△ACD(SAS).
(2)当E点移动2.8厘米时,四边形ACEB为菱形.
理由如下:连BC交AD于O.
∵△ABD≌△ACD(已证)
∴AB=AC,∠BAD=∠ADC
∴AO⊥BO,BO=CO
∵∠B=∠C=90°,AB=8cm,BD=6cm
∴由勾股定理可得AD=10
∵由S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∴BO=4.8
∴由勾股定理可得AO=6.4
∴OD=3.6
∵DE=2.8
∴OD=6.4
∴AO=OD
∴四边形ACEB为菱形(对角线互相垂直平分的四边形为菱形).
点评:本题考查了全等三角形的判定及菱形的判定,解题的关键是牢记菱形的判定定理,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知|a-6|+
+(c-10)2=0,则这个三角形的形状是( )
| b-8 |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
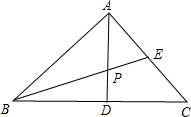 如图,已知△ABC中,∠A=90°,AD是BC边上的高,BE是角平分线,且交AD于P.
如图,已知△ABC中,∠A=90°,AD是BC边上的高,BE是角平分线,且交AD于P.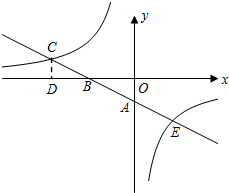 如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=
如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=