题目内容
在等腰梯形ABCD中，AD∥BC，若AD=5，BC=11，梯形的高是4，则梯形的周长 ．
考点：等腰梯形的性质
专题：
分析：作AE⊥BC交BC于点E，先求出BE的长，再运用勾股定理求出AB的长，即可求出梯形的周长．
解答：解：如图，作AE⊥BC交BC于点E，
∵在等腰梯形ABCD中，AD=5，BC=11，
∴BE=（BC-AD）÷2=（11-5）÷2=3，
∵梯形的高是4，
∴AB=
=5，
∴梯形的周长=AB+BC+CD+AD=5+11+5+5=26，
故答案为：26．
∵在等腰梯形ABCD中，AD=5，BC=11，
∴BE=（BC-AD）÷2=（11-5）÷2=3，
∵梯形的高是4，
∴AB=
| 42+32 |
∴梯形的周长=AB+BC+CD+AD=5+11+5+5=26，
故答案为：26．
点评：本题主要考查了等腰梯形的性质，解题的关键是把等腰梯形分成矩形和两个全等的直角三角形．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
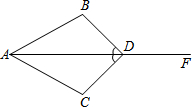如图所示，∠ADB=∠ADC，
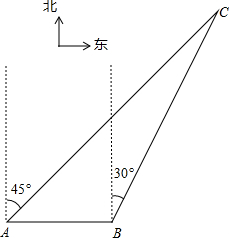如图，我渔政310船在南海海面上沿正东方向匀速航行，在A地观测到我渔船C在东北方向上的我国某传统渔场，若渔政310船航向不变，航行半小时后到达B处，此时观测到我渔船C在北偏东30°方向上．问渔政310船再航行多久，离我渔船C的距离最近？（假设我渔船C捕鱼时移动距离忽略不计，结果不取近似值）
如图，AB是⊙O的弦，OC⊥AB于C．若AB=4
如图，AC是⊙O的直径，点B、点D在⊙O上，∠BAC=48°，则∠ADB=