题目内容
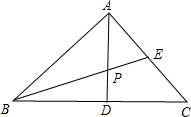 如图,已知△ABC中,∠A=90°,AD是BC边上的高,BE是角平分线,且交AD于P.
如图,已知△ABC中,∠A=90°,AD是BC边上的高,BE是角平分线,且交AD于P.(1)求证:AE=AP.
(2)如果角∠C=30°,AE=1,求AC的长.
考点:等腰三角形的判定与性质
专题:
分析:(1)根据角平分线的性质,可得∠ABE=∠PBD,根据三角形的内角和定理,等式的性质,可得∠AEB与∠BPD的关系,根据等腰三角形的判定,可得答案;
(2)根据直角三角形的性质,可得BE的长度,根据勾股定理,可得AB的长度,根据锐角三角函数,可得答案.
(2)根据直角三角形的性质,可得BE的长度,根据勾股定理,可得AB的长度,根据锐角三角函数,可得答案.
解答:(1)证明:∵BE是∠ABC的角平分线,
∴∠ABE=∠PBD.
∵AD是BC边上的高,
∠PDB=90°.
∵∠AEB、∠A、∠ABE是△ABE的内角,
∴∠AEB=180°-∠A-∠ABE=180°-90°-∠ABE=90°-∠ABE,
∵∠BPD、∠PDB、∠PBD是△PBD的内角,
∴∠BPD=180°-∠PDB-∠PBD=180°-90°-∠PBD=90°-∠PBD,
∴∠AEB=∠BPD.
∵∠APE与∠BPD是对顶角,
∴∠APE=∠AEP,
AE=AP;
(2)解:∠C=30°,
∴∠ABC=60°,.
∵BE平分∠ABC,
∴∠ABE=30°,.
∵AE=1,
∴BE=2AE=2,
由勾股定理,得
AB=
=
.
tan∠ABC=tan 60°=
=
,
AC=
AB=3.
∴∠ABE=∠PBD.
∵AD是BC边上的高,
∠PDB=90°.
∵∠AEB、∠A、∠ABE是△ABE的内角,
∴∠AEB=180°-∠A-∠ABE=180°-90°-∠ABE=90°-∠ABE,
∵∠BPD、∠PDB、∠PBD是△PBD的内角,
∴∠BPD=180°-∠PDB-∠PBD=180°-90°-∠PBD=90°-∠PBD,
∴∠AEB=∠BPD.
∵∠APE与∠BPD是对顶角,
∴∠APE=∠AEP,
AE=AP;
(2)解:∠C=30°,
∴∠ABC=60°,.
∵BE平分∠ABC,
∴∠ABE=30°,.
∵AE=1,
∴BE=2AE=2,
由勾股定理,得
AB=
| 22-12 |
| 3 |
tan∠ABC=tan 60°=
| AC |
| AB |
| 3 |
AC=
| 3 |
点评:本题考查了等腰三角形的判定与性质,利用了等腰三角形的判定,直角三角形的性质,锐角三角函数,题目稍有难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列语句中,不是命题的是( )
| A、两点确定一条直线 |
| B、垂线段最短 |
| C、同位角相等 |
| D、做角A的平分线 |
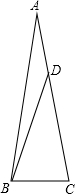 如图,△ABC中,∠A=20°,AB=AC,D是AC上一点,AD=BC,求∠DBA的度数.
如图,△ABC中,∠A=20°,AB=AC,D是AC上一点,AD=BC,求∠DBA的度数. 热气球是用热空气作为浮升气体的气球,人们可以利用它在空中进行飞行.某一天,热气球爱好者小明乘坐热气球在空中A处测得地面一建筑物M的俯角为30°,测得另一建筑物N的俯角为45°(如图),此时热气球离地面的高度为
热气球是用热空气作为浮升气体的气球,人们可以利用它在空中进行飞行.某一天,热气球爱好者小明乘坐热气球在空中A处测得地面一建筑物M的俯角为30°,测得另一建筑物N的俯角为45°(如图),此时热气球离地面的高度为 一个拱形桥洞成抛物线形,它的截面如图.现测得,桥洞顶点O与水面DE的距离为1m,桥洞的水面宽ED=3m,当水位下降到桥洞顶点O与水面AB的距离为3m时,这时水面宽AB是多少m?
一个拱形桥洞成抛物线形,它的截面如图.现测得,桥洞顶点O与水面DE的距离为1m,桥洞的水面宽ED=3m,当水位下降到桥洞顶点O与水面AB的距离为3m时,这时水面宽AB是多少m?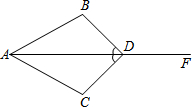 如图所示,∠ADB=∠ADC,
如图所示,∠ADB=∠ADC,