题目内容
12.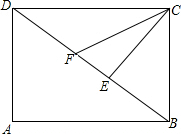 如图,已知平行四边形ABCD中,∠BCD=90°,CE⊥BD于E,CF平分∠DCE与DB交于点F,
如图,已知平行四边形ABCD中,∠BCD=90°,CE⊥BD于E,CF平分∠DCE与DB交于点F,(1)求证:BF=BC;
(2)若AB=4cm,AD=3cm,求CF.
分析 (1)要求证:BF=BC只要证明∠CFB=∠FCB就可以,从而转化为证明∠BCE=∠BDC就可以;
(2)已知AB=4cm,AD=3cm,就是已知BC=BF=3cm,CD=4cm,在直角△BCD中,根据三角形的面积等于$\frac{1}{2}$BD•CE=$\frac{1}{2}$BC•DC,就可以求出CE的长.要求CF的长,可以在直角△CEF中用勾股定理求得.其中EF=BF-BE,BE在直角△BCE中根据勾股定理就可以求出,由此解决问题.
解答 (1)证明:∵平行四边形ABCD中,∠BCD=90°,
∴四边形ABCD是矩形,
∴∠CDB+∠DBC=90°.
∵CE⊥BD,
∴∠DBC+∠ECB=90°.
∴∠ECB=∠CDB.
又∵∠DCF=∠ECF,
∴∠CFB=∠CDB+∠DCF=∠ECB+∠ECF=∠BCF.
∴BF=BC;
(2)解:在Rt△ABD中,由勾股定理得BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5.
又∵BD•CE=BC•DC,
∴CE=$\frac{BC•DC}{BD}$=$\frac{12}{5}$.
∴BE=$\sqrt{B{C}^{2}-C{E}^{2}}$=$\sqrt{{3}^{2}-(\frac{12}{5})^{2}}$=$\frac{9}{5}$.
∴EF=BF-BE=3-$\frac{9}{5}$=$\frac{6}{5}$.
∴CF=$\sqrt{C{E}^{2}+E{F}^{2}}$=$\sqrt{(\frac{12}{5})^{2}+(\frac{6}{5})^{2}}$=$\frac{6\sqrt{5}}{5}$cm.
点评 本题考查矩形的判定与性质,等腰三角形的判定定理,等角对等边,以及勾股定理,三角形面积计算公式的运用,灵活运用已知,理清思路,解决问题.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案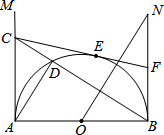 如图,AB是半圆O的直径,射线AM、BN为半圆的切线.在AM上取一点C,连接BC交半圆于点D,连接AD.过O点作BC的垂线ON,与BN相交于点N.过C点作半圆的切线CE,切点为E,与BN相交于点F.当C在AM上移动时(A点除外),设$\frac{BF}{BN}=n$,则n的值为( )
如图,AB是半圆O的直径,射线AM、BN为半圆的切线.在AM上取一点C,连接BC交半圆于点D,连接AD.过O点作BC的垂线ON,与BN相交于点N.过C点作半圆的切线CE,切点为E,与BN相交于点F.当C在AM上移动时(A点除外),设$\frac{BF}{BN}=n$,则n的值为( )| A. | n=$\frac{1}{2}$ | B. | 0<n≤$\frac{3}{4}$ | C. | $\frac{1}{2}$≤n<1 | D. | 无法确定 |
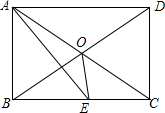 如图所示,在矩形ABCD中,对角线AC、BD相交于点O,∠AOB=60°,AE平分∠BAD,AE交BC于E,求∠AOE的度数.
如图所示,在矩形ABCD中,对角线AC、BD相交于点O,∠AOB=60°,AE平分∠BAD,AE交BC于E,求∠AOE的度数. 如图,M是平行四边形ABCD边AD的中点,且MB=MC,求证:四边形ABCD是矩形.
如图,M是平行四边形ABCD边AD的中点,且MB=MC,求证:四边形ABCD是矩形.