题目内容
12.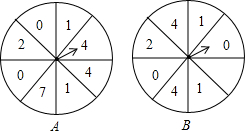 某天,小明和小华利用“争1点”的游戏来预测一场足球比赛的冠军.如图,两个可以自由转动的转盘A,B,每个转盘被分成8个相等的扇形,其规则如下:①小明自由转动转盘A,同时小华自由转动转盘B;②转盘停止后,指针指向几就顺时针走几格,得到一个数字(若转盘A中指针指向2,则按顺时针方向走2格得到数字1);③若最终得到的数字是1,则自己所支持的球队称为预测冠军(若双方都得到1,则重新开始).这个游戏对双方公平吗?请说明理由.
某天,小明和小华利用“争1点”的游戏来预测一场足球比赛的冠军.如图,两个可以自由转动的转盘A,B,每个转盘被分成8个相等的扇形,其规则如下:①小明自由转动转盘A,同时小华自由转动转盘B;②转盘停止后,指针指向几就顺时针走几格,得到一个数字(若转盘A中指针指向2,则按顺时针方向走2格得到数字1);③若最终得到的数字是1,则自己所支持的球队称为预测冠军(若双方都得到1,则重新开始).这个游戏对双方公平吗?请说明理由.
分析 列表得出所有等可能的情况数,找出小明和小华获胜的情况,求出各自的概率,比较即可.
解答 解:这个游戏公平,理由为:
列表如下:
| 4 | 4 | 1 | 7 | 0 | 2 | 0 | 1 | |
| 0 | (4,0) | (4,0) | (1,0) | (7,0) | (0,0) | (2,0) | (0,0) | (1,0) |
| 7 | (4,7) | (4,7) | (1,7) | (7,7) | (0,7) | (2,7) | (0,7) | (1,7) |
| 0 | (4,0) | (4,0) | (1,0) | (7,0) | (0,0) | (2,0) | (0,0) | (1,0) |
| 4 | (4,4) | (4,4) | (1,4) | (7,4) | (0,4) | (2,4) | (0,4) | (1,4) |
| 1 | (4,1) | (4,1) | (1,1) | (7,1) | (0,1) | (2,1) | (0,1) | (1,1) |
| 1 | (4,1) | (4,1) | (1,1) | (7,1) | (0,1) | (2,1) | (0,1) | (1,1) |
| 4 | (4,4) | (4,4) | (1,4) | (7,4) | (0,4) | (2,4) | (0,4) | (1,4) |
| 2 | (4,2) | (4,2) | (1,2) | (7,2) | (0,2) | (2,2) | (0,2) | (1,2) |
∴P(小明获胜)=P(小华获胜)=$\frac{12}{64}=\frac{3}{16}$,
则这个游戏公平.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.游戏双方获胜的概率相同,游戏就公平,否则游戏不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
7.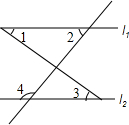 如图,下列判断正确的是( )
如图,下列判断正确的是( )
 如图,下列判断正确的是( )
如图,下列判断正确的是( )| A. | 若∠1+∠2=180°,则l1∥l2 | B. | 若∠2=∠3,则l1∥l2 | ||
| C. | 若∠1+∠2+∠3=180°,则l1∥l2 | D. | 若∠2+∠4=180°,则l1∥l2 |
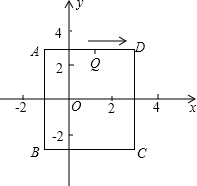 如图,在平面直角坐标系中,长方形ABCD的边BC∥x轴,如果A点坐标是(-1,2$\sqrt{2}$),C点坐标是(3,-2$\sqrt{2}$).
如图,在平面直角坐标系中,长方形ABCD的边BC∥x轴,如果A点坐标是(-1,2$\sqrt{2}$),C点坐标是(3,-2$\sqrt{2}$).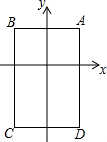 在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-….的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(0,-2).
在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-….的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(0,-2).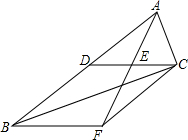 如图,CD是△ABC的中线,点E是AF的中点,CF∥AB.
如图,CD是△ABC的中线,点E是AF的中点,CF∥AB.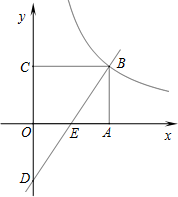 矩形ABCO如图放置,点A,C在坐标轴上,点B在第一象限,一次函数y=kx-3的图象过点B,分别交x轴、y轴于点E、D,已知C(0,3)且S△BCD=12.
矩形ABCO如图放置,点A,C在坐标轴上,点B在第一象限,一次函数y=kx-3的图象过点B,分别交x轴、y轴于点E、D,已知C(0,3)且S△BCD=12.