题目内容
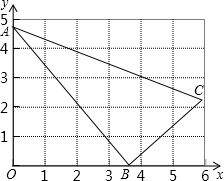 如图,△ABC中,∠ABC=90°,A(0,4.8),B(3.6,0).BC=3,
如图,△ABC中,∠ABC=90°,A(0,4.8),B(3.6,0).BC=3,(1)AB=
(2)当△ABC形状大小不变,A、B两点沿y,x轴滑动过程中,OC的最大值为
(3)点P从A点出发沿A-B-C路径向终点运动,终点为C点;点Q从B点出发沿B-C-A路径向终点运动,终点为A点.点P和Q分别以3和1的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥x轴于E,QF⊥x轴于F.问:点P运动多少时间时,△PEB与△QFB全等?请说明理由.(A、B不与原点重合)
考点:勾股定理,坐标与图形性质,全等三角形的判定,直角三角形斜边上的中线
专题:
分析:(1)根据点A、B的坐标求出OA、OB,再利用勾股定理列式计算即可得解;
(2)取AB的中点D,连接OD、CD,再根据直角三角形斜边上的中线等于斜边的一半求出OD,利用勾股定理列式求出CD,然后根据三角形的任意两边之和大于第三边判断出O、D、C三点共线时OC最大;
(3)求出点P、Q到达点C的时间,然后分点P在AB上和点P在BC上两种情况,根据全等三角形对应边相等可得PB=QB,然后列方程求解即可.
(2)取AB的中点D,连接OD、CD,再根据直角三角形斜边上的中线等于斜边的一半求出OD,利用勾股定理列式求出CD,然后根据三角形的任意两边之和大于第三边判断出O、D、C三点共线时OC最大;
(3)求出点P、Q到达点C的时间,然后分点P在AB上和点P在BC上两种情况,根据全等三角形对应边相等可得PB=QB,然后列方程求解即可.
解答:解:(1)∵A(0,4.8),B(3.6,0),
∴OA=4.8,OB=3.6,
∴AB=
=
=6;
故答案为:6;

(2)取AB的中点D,连接OD、CD,
∵△AOB是直角三角形,
∴OD=BD=
AB=
×6=3,
在Rt△BCD中,CD=
=
=3
,
当O、D、C三点共线时OC最大,最大值为3
+3;
故答案为:3
+3;
(3)∵(6+3)÷3=3,
3÷1=3,
∴点P、Q到达点C的时间都是3秒,
点P在AB上时,∵△PEB≌△BFQ,
∴PB=QB,
∴6-3t=t,
解得t=
,
点P在BC上时,∵△PEB≌△QFB,
∴PB=QB,
∴3t-6=t,
解得t=3,
综上所述,点P运动
秒或3秒时,△PEB与△QFB全等.
∴OA=4.8,OB=3.6,
∴AB=
| OA2+OB2 |
| 4.82+3.62 |
故答案为:6;

(2)取AB的中点D,连接OD、CD,
∵△AOB是直角三角形,
∴OD=BD=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△BCD中,CD=
| BC2+BD2 |
| 32+32 |
| 2 |
当O、D、C三点共线时OC最大,最大值为3
| 2 |
故答案为:3
| 2 |
(3)∵(6+3)÷3=3,
3÷1=3,
∴点P、Q到达点C的时间都是3秒,
点P在AB上时,∵△PEB≌△BFQ,
∴PB=QB,
∴6-3t=t,
解得t=
| 3 |
| 2 |
点P在BC上时,∵△PEB≌△QFB,
∴PB=QB,
∴3t-6=t,
解得t=3,
综上所述,点P运动
| 3 |
| 2 |
点评:本题考查了勾股定理,坐标与图形性质,全等三角形的性质,直角三角形斜边上的中线等于斜边的一半的性质,难点在于(2)确定出OC最大时的情况,(3)判断出P、Q同时到达点C是解题的关键.

练习册系列答案
相关题目
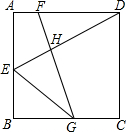 如图,在正方形ABCD中,点E是AB上一点,G是BC上一点,FG⊥DE交于点H,FG=DE,求证:FD+EG≥
如图,在正方形ABCD中,点E是AB上一点,G是BC上一点,FG⊥DE交于点H,FG=DE,求证:FD+EG≥
 如图所示,△ABC为直角三角形,∠ACB=90°,若∠A=30°,那么线段BC、AB的长度有何数量关系?
如图所示,△ABC为直角三角形,∠ACB=90°,若∠A=30°,那么线段BC、AB的长度有何数量关系?