题目内容
已知AB是⊙O的直径,C为⊙O上的一点,
与
的长度比是1:2,弦BC=12cm,则⊙O半径为 cm.
 |
| AC |
 |
| CB |
考点:圆周角定理,勾股定理,圆心角、弧、弦的关系
专题:
分析:连结OC.首先由圆周角定理及圆心角、弧、弦的关系定理得出∠ACB=90°,∠AOC=
×180°=60°,又OA=OC,那么△AOC是等边三角形,于是∠A=60°,然后在直角△ABC中利用正弦函数的定义即可求出AB.
| 1 |
| 3 |
解答: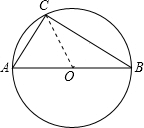 解:如图,连结OC.
解:如图,连结OC.
∵AB是⊙O的直径,C为⊙O上的一点,
与
的长度比是1:2,
∴∠ACB=90°,∠AOC=
×180°=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴∠A=60°,
∴AB=
=
=8
(cm).
故答案为8
.
 解:如图,连结OC.
解:如图,连结OC.∵AB是⊙O的直径,C为⊙O上的一点,
 |
| AC |
 |
| CB |
∴∠ACB=90°,∠AOC=
| 1 |
| 3 |
∵OA=OC,
∴△AOC是等边三角形,
∴∠A=60°,
∴AB=
| BC |
| sin∠A |
| 12 | ||||
|
| 3 |
故答案为8
| 3 |
点评:本题考查了圆周角定理,圆心角、弧、弦的关系定理,等边三角形的判定与性质,正弦函数的定义,难度适中.得出∠AOC=60°是解题的关键.

练习册系列答案
相关题目
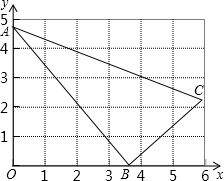 如图,△ABC中,∠ABC=90°,A(0,4.8),B(3.6,0).BC=3,
如图,△ABC中,∠ABC=90°,A(0,4.8),B(3.6,0).BC=3,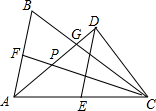 如图,在△ABC中,过C作∠BAC的平分线AD的垂线,垂足为D,AD交BC于G,DE∥AB交AC于E.
如图,在△ABC中,过C作∠BAC的平分线AD的垂线,垂足为D,AD交BC于G,DE∥AB交AC于E.