题目内容
如图,正方形ABCD中,E为BC边中点.
(1)如图1,F为BE中点,求证:∠ADF=2∠CDE;
(2)如图2,将△DCE沿DE翻折得到△DGE,EG的延长线交AB于M,DG的延长线交AB于N,求:求
的值.

(1)如图1,F为BE中点,求证:∠ADF=2∠CDE;
(2)如图2,将△DCE沿DE翻折得到△DGE,EG的延长线交AB于M,DG的延长线交AB于N,求:求
| AN |
| CN |

考点:四边形综合题
专题:
分析:(1)取AB中点H,连接DH,FH,根据正方形的性质得出AB=BC=CD=AD,AH=CE=
AB,设BF=a,则AB=AD=BC=4a,CF=3a,AH=BH=2a,求出△DFH是直角三角形,根据
=
=
求出△ADH∽△HDF,推出∠ADH=∠FDH,求出△HAD≌△ECD,∠CDE=∠ADH=∠FDH,求出∠ADF=2∠ADH=2∠CDE;
(2)延长EG交AB于M,交DA于H,连接DM,根据翻折得出CE=EG=2a,DG=DC=AD=4a,∠DEC=∠DEG,∠DGE=∠DCE=90°,在Rt△DGH中,DH2=GH2+DG2,求出GH=3a,证Rt△ADM≌Rt△DGM,推出AM=MG,证△AMH≌△GMN,推出MH=MN,求出AN=GH=3a,BN=AB-AN=a,根据勾股定理求出CN,即可得出答案.
| 1 |
| 2 |
| AD |
| AH |
| 4a |
| 2a |
| DH |
| FH |
(2)延长EG交AB于M,交DA于H,连接DM,根据翻折得出CE=EG=2a,DG=DC=AD=4a,∠DEC=∠DEG,∠DGE=∠DCE=90°,在Rt△DGH中,DH2=GH2+DG2,求出GH=3a,证Rt△ADM≌Rt△DGM,推出AM=MG,证△AMH≌△GMN,推出MH=MN,求出AN=GH=3a,BN=AB-AN=a,根据勾股定理求出CN,即可得出答案.
解答:(1)证明:如图1,取AB中点H,连接DH,FH,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,AH=CE=
AB,
∵F是BE的中点,
∴BF=EF=
CE=
BC,
设BF=a,则AB=AD=BC=4a,
∴CF=3a,AH=BH=2a,
∴DH2=AH2+AD2=20a2,FH2=BH2+BF2=5a2,DF2=CF2+DC2=25a2,
∴DF2=DH2+FH2,
∴△DFH是直角三角形,
∵
=
=2=
=
,
∴△ADH∽△HDF,
∴∠ADH=∠FDH,
∵四边形ABCD是正方形,
∴∠A=∠C=90°,
在△HAD和△ECD中
∴△HAD≌△ECD,
∴∠CDE=∠ADH=∠FDH,
∴∠ADF=∠ADH+∠FDH=2∠ADH=2∠CDE;
(2)解:如图2,延长EG交AB于M,交DA于H,连接DM,
∵△DCE沿DE翻折到△DGE,
∴△DCE≌△DGE,
∴CE=EG=2a,DG=DC=AD=4a,∠DEC=∠DEG,∠DGE=∠DCE=90°,
∵AD∥BC,
∴∠HDE=∠DEC=∠DEG,
∴DH=EH=GH+GE=GH+2a,
∴在Rt△DGH中,DH2=GH2+DG2,
即(GH+2a)2=GH2+(4a)2,
解得:GH=3a,
∵∠DAM=∠DGM=90°,
∴在Rt△ADM和Rt△DGM中
∴Rt△ADM≌Rt△DGM,
∴AM=MG,
在△AMH和△GMN中
∴△AMH≌△GMN,
∴MH=MN,
∴AN=AM+MN=MG+MH=GH=3a,
∴BN=AB-AN=a,
∴CN=
=
a,
∴
=
=
.

∵四边形ABCD是正方形,
∴AB=BC=CD=AD,AH=CE=
| 1 |
| 2 |
∵F是BE的中点,
∴BF=EF=
| 1 |
| 2 |
| 1 |
| 4 |
设BF=a,则AB=AD=BC=4a,
∴CF=3a,AH=BH=2a,
∴DH2=AH2+AD2=20a2,FH2=BH2+BF2=5a2,DF2=CF2+DC2=25a2,
∴DF2=DH2+FH2,
∴△DFH是直角三角形,
∵
| AD |
| AH |
| 4a |
| 2a |
| ||
|
| DH |
| FH |
∴△ADH∽△HDF,
∴∠ADH=∠FDH,
∵四边形ABCD是正方形,
∴∠A=∠C=90°,
在△HAD和△ECD中
|
∴△HAD≌△ECD,
∴∠CDE=∠ADH=∠FDH,
∴∠ADF=∠ADH+∠FDH=2∠ADH=2∠CDE;
(2)解:如图2,延长EG交AB于M,交DA于H,连接DM,

∵△DCE沿DE翻折到△DGE,
∴△DCE≌△DGE,
∴CE=EG=2a,DG=DC=AD=4a,∠DEC=∠DEG,∠DGE=∠DCE=90°,
∵AD∥BC,
∴∠HDE=∠DEC=∠DEG,
∴DH=EH=GH+GE=GH+2a,
∴在Rt△DGH中,DH2=GH2+DG2,
即(GH+2a)2=GH2+(4a)2,
解得:GH=3a,
∵∠DAM=∠DGM=90°,
∴在Rt△ADM和Rt△DGM中
|
∴Rt△ADM≌Rt△DGM,
∴AM=MG,
在△AMH和△GMN中
|
∴△AMH≌△GMN,
∴MH=MN,
∴AN=AM+MN=MG+MH=GH=3a,
∴BN=AB-AN=a,
∴CN=
| BN2+BC2 |
| 17 |
∴
| AN |
| CN |
| 3a | ||
|
3
| ||
| 17 |
点评:本题考查了全等三角形的性质和判定,勾股定理,正方形的性质的应用,题目比较好,但是难度偏大.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
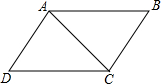 如图,已知△ABC≌△CDA,A和C,D和B分别是对应点,如果AB=7cm,AD=
如图,已知△ABC≌△CDA,A和C,D和B分别是对应点,如果AB=7cm,AD=6cm,AC=4cm,则DC的长为( )
| A、6cm | B、7cm |
| C、4cm | D、不确定 |
在-
,
,
4.
,
,
,这几个数中无理数有( )个.
| 22 |
| 7 |
| 3 | 9 |
| 25 |
| • |
| 2 |
| π |
| 2 |
| 0.4 |
| A、4 | B、3 | C、2 | D、1 |
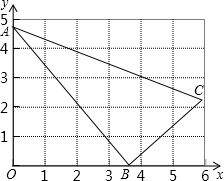 如图,△ABC中,∠ABC=90°,A(0,4.8),B(3.6,0).BC=3,
如图,△ABC中,∠ABC=90°,A(0,4.8),B(3.6,0).BC=3,