题目内容

正方形ABCD的边长为4，点E是正方形边上的点，AE=5，BF⊥AE，垂足为点F，求BF的长．
考点：正方形的性质
专题：
分析：利用勾股定理列式求出BE，再利用△ABE的面积列式计算即可得解．
解答：解：如图，由勾股定理得，BE=
AE2-AB2
=
52-42
=3，
∵BF⊥AE，
∴S△ABE=
1
2
AE•BF=
1
2
AB•BE，
即
1
2
×5•BF=
1
2
×4×3，
解得BF=
12
5
．
点评：本题考查了正方形的性质，勾股定理，三角形的面积，熟记性质是解题的关键，作出图形更形象直观．
练习册系列答案
相关题目
某中学举行数学知识竞赛，所有参赛学生分别设有一、二、三等奖和纪念奖，获奖情况已汇制成如图所示的两幅不完整的统计图，根据图中所经信息解答下列问题：

（1）二等奖所占的比例是多少？
（2）这次数学知识竞赛获得二等奖人数是多少？
（3）请将条形统计图补充完整．
如图，边长为1的正方形ABCD绕点A逆时针旋转45°到正方形AB′C′D′，图中重合部分的面积为
 
．
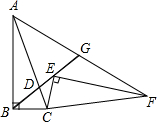如图，在Rt△ABC中，∠B=90°，sin∠BAC=
1
3
，点D是AC上一点，且BC=BD=2，将Rt△ABC绕点C旋转到Rt△FEC的位置，并使点E在射线BD上，连结AF交射线BD于点G，则AG的长为（　　）
A、
14
3
B、3
2
+
1
2
C、3
3
-
1
2
D、
9
2
4的算术平方根是（　　）
A、2
B、-2
C、±2
D、a2+a2=a4
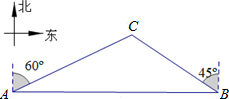如图，一天，我国一渔政船航行到A处时，发现正东方向的我领海区域B处有一可疑渔船，正在以12海里/小时的速度向西北方向航行，我渔政船立即沿北偏东60°方向航行，1.5小时后，在我领海区域的C处截获可疑渔船，问我渔政船的航行路程是多少海里？（结果精确到0.1海里，
2
≈1.414）
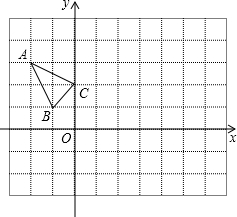△ABC在平面直角坐标系xOy中的位置如图所示，点A的坐标为（-2，3），点B的坐标为（-1，1），点C的坐标为（0，2）．
（1）作△ABC关于点C成中心对称的△A1BlCl．
（2）将△A1BlCl向右平移4个单位，作出平移后的△A2B2C2．
（3）点P是x轴上的一点，并且使得PA1+PC2的值最小，则点P的坐标为（
 
，
 
）．
阅读材料：
例：说明代数式
x2+1
+
(x-3)2+4
的几何意义，并求它的最小值．
解：
x2+1
+
(x-3)2+4
=
(x-0)2+12
+
(x-3)2+22
，如图，建立平面直角坐标系，点P（x，0）是x轴上一点，则
(x-0)2+12
可以看成点P与点A（0，1）的距离，
(x-3)2+22
可以看成点P与点B（3，2）的距离，所以原代数式的值可以看成线段PA与PB长度之和，它的最小值就是PA+PB的最小值．
设点A关于x轴的对称点为A′，则PA=PA′，因此，求PA+PB的最小值，只需求PA′+PB的最小值，而点A′、B间的直线段距离最短，所以PA′+PB的最小值为线段A′B的长度．为此，构造直角三角形A′CB，因为A′C=3，CB=3，所以A′B=3
2
，即原式的最小值为3
2
．
根据以上阅读材料，解答下列问题：
（1）代数式
(x-1)2+1
+
(x-2)2+9
的值可以看成平面直角坐标系中点P（x，0）与点A（1，1）、点B
 
的距离之和．（填写点B的坐标）
（2）求代数式
x2+49
+
x2-12x+37
的最小值．
图1、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，点A、B、C在小正方形的顶点上，请图1、图2中各画一个四边形，满足以下要求：
（1）在图1中，以AB、BC为边画四边形ABCD，点D在小正方形的顶点上，且此四边形有两组角互补且是非对称图形；
（2）在图2中以以AB、BC为边画四边形ABCD，点D在小正方形的顶点上，且此四边形有两组角互补且是轴对称图形．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网