题目内容
5.【问题提出】我们知道对于任何一个封闭的平面图形.是否存在既平分周长,又平分面积的直线.
【问题探究】
(1)请在图1的三个图形中,分别做一条直线,使这条直线既平分周长,又平分面积.

(2)如图2,在Rt△ABC中,∠A=90°,AB=3,AC=4,是否存在过AB上的点M的直线,使它既平分△ABC的周长,又平分△ABC的面积?若存在,求出AM的长;若不存在,请说明理由.
【问题解决】
(3)如图3,四边形ABCD是某市将要筹建的高新技术开发区用地示意图,其中AB=AD=9,BC=5,CD=13,∠A=90°.为了方便驻区单位,准备修一条笔直的道路(路宽不计),使这条路所在的直线既平分四边形ABCD的周长,又平分四边形ABCD的面积.并且要求路的一个出口在DC边上,你认为这样的路是否存在?若存在,请求出路的另一个出口与点A的距离;若不存在,请说明理由.
分析 (1)①根据圆的特征,可得圆的直径既平分圆的周长,又平分圆的面积.
②根据平行四边形的特征,可得平行四边形的对角线既平分它的周长,又平分它的面积.
③根据等腰三角形的特征,可得等腰三角形底边上的高既平分它的周长,又平分它的面积.
(2)存在过AB的点M的直线,使它既平分△ABC的周长,又平分△ABC的面积;首先设AM=x,则BP=3-x,CQ=2-x,BQ=x+3,然后根据△BMQ的面积等于△ABC的面积的一半,求出AM的值是多少即可.
(3)不存在这样的路EF,使这条路所在的直线既平分四边形ABCD的周长,又平分四边形ABCD的面积.首先设AE=x,则BE=9-x,DF=36÷2-x-9=9-x,CF=13-(9-x)=x+4,然后根据四边形AEFD的面积等于四边形ABCD的面积的一半,列出方程,根据方程的解的情况判断即可.
解答 解:(1)根据分析,可得 .
.
(2)如图2, ,
,
存在过AB的点M的直线,使它既平分△ABC的周长,又平分△ABC的面积,
∵在Rt△ABC中,∠A=90°,AB=3,AC=4,
∴BC=$\sqrt{{3}^{2}{+4}^{2}}$=5,
设AM=x,直线MQ既平分△ABC的周长,又平分△ABC的面积,
则BM=3-x,CQ=(3+4+5)÷2-x-4=2-x,BQ=5-(2-x)=x+3,
∵${S}_{△ABC}=\frac{1}{2}AB•AC=\frac{1}{2}×3×4=6$,
∴S△BMQ=6÷2=3,
∴$\frac{3-x}{3}×\frac{x+3}{5}×6=3$,
解得x=$\frac{\sqrt{6}}{2}$或-$\frac{\sqrt{6}}{2}$(舍弃),
∴存在过AB上的点M的直线,使它既平分△ABC的周长,又平分△ABC的面积,此时AM=$\frac{\sqrt{6}}{2}$.
(3)如图3,作CM⊥AD于点M,FN⊥AD于点N, ,
,
不存在这样的路EF,使这条路所在的直线既平分四边形ABCD的周长,又平分四边形ABCD的面积.
∵AB=AD=9,BC=5,CD=13,
∴四边形ABCD的周长为:9+9+5+13=36;
设AM=a,则DM=9-a,CM=b,
则$\left\{\begin{array}{l}{{a}^{2}{+(b-9)}^{2}{=5}^{2}}\\{{(9-a)}^{2}{+b}^{2}{=13}^{2}}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=4}\\{b=12}\end{array}\right.$
∴S四边形ABCD=(9+12)×4÷2+12×(9-4)÷2=72
设AE=x,
则BE=9-x,DF=36÷2-x-9=9-x,CF=13-(9-x)=x+4,
∵CM⊥AD,FN⊥AD,
∴FN∥CM,
∴$\frac{FN}{CM}=\frac{FD}{CD}$=$\frac{ND}{MD}$,
∴$\frac{FN}{12}=\frac{9-x}{13}$=$\frac{ND}{9-3}=\frac{ND}{6}$,
解得FN=$\frac{12}{13}(9-x)$,ND=$\frac{6}{13}(9-x)$,
∴${S}_{四边形AEFD}=[x+\frac{12}{13}(9-x)]$×$[9-\frac{6}{13}(9-x)]$÷2+$\frac{12}{13}(9-x)$×$\frac{6}{13}(9-x)$÷2=72÷2=36
整理,可得
52x2-390x+819=0,
△=3902-4×52×819=-18252<0,
∴x无解,
∴不存在这样的路EF,使这条路所在的直线既平分四边形ABCD的周长,又平分四边形ABCD的面积.
点评 此题主要考查了作图-应用与设计作图问题,要熟练掌握,解答此类问题的关键是首先要理解题意,弄清问题中对所作图形的要求,然后结合对应几何图形的性质和基本作图的方法作图.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\sqrt{2+x}$ | B. | $\sqrt{2-x}$ | C. | $\sqrt{\frac{1}{x-2}}$ | D. | $\sqrt{x-2}$ |
| A. | $\left\{\begin{array}{l}a=3\\ b=-2\end{array}\right.$ | B. | $\left\{\begin{array}{l}a=-1\\ b=3\end{array}\right.$ | C. | $\left\{\begin{array}{l}a=0\\ b=2\end{array}\right.$ | D. | $\left\{\begin{array}{l}a=1\\ b=2\end{array}\right.$ |
| A. | 3.7×10-5 | B. | 37×10-5 | C. | 3.7×10-6 | D. | 0.37×10-5 |
| A. | 6.397×104 | B. | 6.397×105 | C. | 6.397×106 | D. | 6.397×107 |
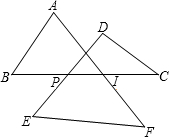 如图,求:∠A+∠B+∠C+∠D+∠E+∠F的度数.
如图,求:∠A+∠B+∠C+∠D+∠E+∠F的度数.
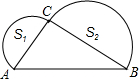 如图,已知在Rt△ABC中,∠BCA=90°,AB=10,分别以AC、BC为直径作半圆,面积分别记为S1,S2,则S1+S2=12.5π.
如图,已知在Rt△ABC中,∠BCA=90°,AB=10,分别以AC、BC为直径作半圆,面积分别记为S1,S2,则S1+S2=12.5π.