题目内容

已知β是锐角，且sin（β+15°）=
3
2
，计算
8
-4cosβ-tan45°+tan230°．
考点：特殊角的三角函数值
专题：
分析：利用特殊角的三角函数值得出β的度数，再化简各数求出即可．
解答：解：∵sin（β+15°）=
3
2
，
∴β+15°=60°，
∴β=45°，
∴
8
-4cosβ-tan45°+tan230°
=2
2
-4×
2
2
-1+（
3
3
）2
=-
2
3
．
点评：此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键．
练习册系列答案
相关题目
（1）问题情境：
勾股定理是一条古老的数学定理，它有很多种证明方法，我国汉代数学家赵爽根据弦图，借助“数形关系”利用面积法进行证明，而以刘徽的“青朱出入图”为代表的“无字证明”也颇为神奇，证明不需用任何数学符号和文字，整个证明单靠移动几块图形而得出．
如图1和2，将4个全等的直角三角形拼成边长为（a+b）的正方形，使中间留下一个边长c的空白正方形，画出边长为（a+b）正方形，在移动三角形至图2所示的位置中，于是留下了边长分别为a和b的两个空白正方形．则图1和图2中的白色部分面积必定相等，即
 
；
（2）尝试证明：实际上只需图2的“一半”即可用“数形关系”和面积法证明，美国总统伽菲尔德在1876年利用图3证明了勾股定理，请你来试一试，借助图3完成证明：
（3）问题拓展：已知Rt△ABC的两直角边分别为a，b，斜边为c，求证：
a+b
c
≤
2
．
如图，晓明在墙上挂了一面镜子AB，调整好标杆CD，正好通过标杆顶部在镜子上边缘A处看到标杆顶端E的影子．已知AB=2m，CD=1.5m，BD=2m，BF=20m，求旗杆EF的高度．
在平面直角坐标系中，位于第四象限的点是（　　）
A、（1，-2）
B、（2，1）
C、（-2，1）
D、（-1，-3）
不等式组
2-4x≤x-8
1
3
x+2＜
x
2
的解集是
 
．
在下列图形的特征中，平行四边形不一定具有的是（　　）
A、对角相等
B、对角互补
C、邻角互补
D、内角和是180度
先化简，再求值：
m+1
2m2-2m
．（
2m
m+1
）2-（
1
m-1
-
1
m+1
），其中m=
3
．
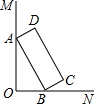如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM、ON上，当B在边ON上运动时，A随之在边OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1．运动过程中，点C到点O的最大距离是（　　）
A、
145
5
B、
2
+1
C、
5
D、
5
2
已知：如图，点B是线段AD的中点，C是线段BD的中点，BC=2cm，那么线段AD等于（　　）
A、2cmB、4cm
C、6cmD、8cm

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网