题目内容
(1)问题情境:
勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,借助“数形关系”利用面积法进行证明,而以刘徽的“青朱出入图”为代表的“无字证明”也颇为神奇,证明不需用任何数学符号和文字,整个证明单靠移动几块图形而得出.
如图1和2,将4个全等的直角三角形拼成边长为(a+b)的正方形,使中间留下一个边长c的空白正方形,画出边长为(a+b)正方形,在移动三角形至图2所示的位置中,于是留下了边长分别为a和b的两个空白正方形.则图1和图2中的白色部分面积必定相等,即 ;
(2)尝试证明:实际上只需图2的“一半”即可用“数形关系”和面积法证明,美国总统伽菲尔德在1876年利用图3证明了勾股定理,请你来试一试,借助图3完成证明:
(3)问题拓展:已知Rt△ABC的两直角边分别为a,b,斜边为c,求证:
≤
.

勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,借助“数形关系”利用面积法进行证明,而以刘徽的“青朱出入图”为代表的“无字证明”也颇为神奇,证明不需用任何数学符号和文字,整个证明单靠移动几块图形而得出.
如图1和2,将4个全等的直角三角形拼成边长为(a+b)的正方形,使中间留下一个边长c的空白正方形,画出边长为(a+b)正方形,在移动三角形至图2所示的位置中,于是留下了边长分别为a和b的两个空白正方形.则图1和图2中的白色部分面积必定相等,即
(2)尝试证明:实际上只需图2的“一半”即可用“数形关系”和面积法证明,美国总统伽菲尔德在1876年利用图3证明了勾股定理,请你来试一试,借助图3完成证明:
(3)问题拓展:已知Rt△ABC的两直角边分别为a,b,斜边为c,求证:
| a+b |
| c |
| 2 |

考点:勾股定理的证明
专题:
分析:(1)结合图形可知得到c2=a2+b2;
(2)可以利用梯形减去两个黑色直角三角形的面积,整理可得到c2=a2+b2,可证得结论;
(3)可把不等式两边平方,再结合勾股定理可证得.
(2)可以利用梯形减去两个黑色直角三角形的面积,整理可得到c2=a2+b2,可证得结论;
(3)可把不等式两边平方,再结合勾股定理可证得.
解答:(1)解:在图1中,白色部分为边为c的正方形,其面积为c2,
在图2中,白色部分为边长分别为a和b的两个正方形,其面积和为a2+b2,
而a、b、c是直角三角形的三边,所以有c2=a2+b2,
故答案为:c2=a2+b2;
(2)证明:∵S白三角形=S梯形-2S黑三角形,
∴
c2=
(a+b)(a+b)-2×
ab,
即c2=a2+b2;
(3)证明:∵0≤(a-b)2,
∴2ab≤a2+b2,
∴a2+b2+2ab≤2(a2+b2),
∵a2+b2=c2,
∴(a+b)2≤2c2,
∴(
)2≤2,
∴
≤
.
在图2中,白色部分为边长分别为a和b的两个正方形,其面积和为a2+b2,
而a、b、c是直角三角形的三边,所以有c2=a2+b2,
故答案为:c2=a2+b2;
(2)证明:∵S白三角形=S梯形-2S黑三角形,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即c2=a2+b2;
(3)证明:∵0≤(a-b)2,
∴2ab≤a2+b2,
∴a2+b2+2ab≤2(a2+b2),
∵a2+b2=c2,
∴(a+b)2≤2c2,
∴(
| a+b |
| c |
∴
| a+b |
| c |
| 2 |
点评:本题主要考查勾股定理的证明和应用,等积法是证明勾股定理常用的方法,注意数形结合思想的应用.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
下面在函数y=2x-1的图象上的点是( )
| A、(-2.5,-4) |
| B、(1,3) |
| C、(2.5,4) |
| D、(-1,3) |
已知点P1(x1,y2),P2(x2,y2)是一次函数y=3x+4图象上的两个点,且y1>y2;则x1与x2的大小关系是( )
| A、x1>x2 |
| B、x1<x2 |
| C、x1≤x2 |
| D、x1=x2 |
 一个正方体的每个面上都标注了一个汉字,如图是它的一种表面展开图,在这个正方体表面上“更”字对面上标注的汉字是( )
一个正方体的每个面上都标注了一个汉字,如图是它的一种表面展开图,在这个正方体表面上“更”字对面上标注的汉字是( )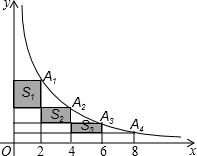 在反比例函数y=
在反比例函数y=