题目内容
16. 如图,已知CD是⊙O的直径,∠EOD=75°,AE交⊙O于B,且AB=OC,则∠A的度数为25°.
如图,已知CD是⊙O的直径,∠EOD=75°,AE交⊙O于B,且AB=OC,则∠A的度数为25°.
分析 连接OB,在△AOB和△AOE中利用三角形的外角的性质,外角等于不相邻的两个内角的和即可求解.
解答 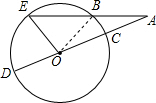 解:连接OB.
解:连接OB.
设∠A=x°,
∵AB=OC,OB=OC,
∴∠BOA=∠A=x°,
∴∠EBO=∠A+∠BOA=2x°,
又∵OB=OE,
∴∠E=∠EBO=2x°,
∵∠EOD=∠E+∠A=2x+x=3x°,
即3x=75,
解得:x=25.
则∠A的度数是25°.
故答案是:25°.
点评 本题考查了三角形的外角的性质以及等腰三角形的性质,正确根据等腰三角形的性质得到∠A、∠E与以及∠EOD的关系是本题的关键.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
8. 综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )
综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )
 综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )
综合实践活动中,同学们做泥塑工艺制作.小明将各同学的作品完成情况绘成了如图的条形统计图.根据图表,我们可以知道平均每个学生完成作品( )| A. | 12件 | B. | 8.625件 | C. | 8.5件 | D. | 9件 |
5.下列函数中,y是x的反比例函数的是( )
| A. | y=x-1 | B. | y=$\frac{8}{{x}^{2}}$ | C. | $\frac{y}{x}$=2 | D. | y=$\frac{1}{2x}$ |
6. 已知二次函数y=2x2+bx+1,当b取不同的值时,其图象构成一个“抛物线系”,如图中的实线型抛物线分别是b取三个不同的值时二次函数的图象,它们的顶点在一条抛物线上(图中虚线型抛物线),则这条虚线型抛物线的解析式是( )
已知二次函数y=2x2+bx+1,当b取不同的值时,其图象构成一个“抛物线系”,如图中的实线型抛物线分别是b取三个不同的值时二次函数的图象,它们的顶点在一条抛物线上(图中虚线型抛物线),则这条虚线型抛物线的解析式是( )
 已知二次函数y=2x2+bx+1,当b取不同的值时,其图象构成一个“抛物线系”,如图中的实线型抛物线分别是b取三个不同的值时二次函数的图象,它们的顶点在一条抛物线上(图中虚线型抛物线),则这条虚线型抛物线的解析式是( )
已知二次函数y=2x2+bx+1,当b取不同的值时,其图象构成一个“抛物线系”,如图中的实线型抛物线分别是b取三个不同的值时二次函数的图象,它们的顶点在一条抛物线上(图中虚线型抛物线),则这条虚线型抛物线的解析式是( )| A. | y=-x2+1 | B. | y=-2x2+1 | C. | y=-$\frac{1}{2}$x2+1 | D. | y=-4x2+1 |
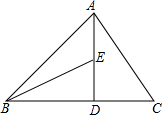 如图,在△ABC中,AD⊥BC于点D,AD=BD,DC=DE,∠C=60°,∠ABD=45°,求∠ABE的度数.
如图,在△ABC中,AD⊥BC于点D,AD=BD,DC=DE,∠C=60°,∠ABD=45°,求∠ABE的度数. 如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.
如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点,且EG、FH交于点O.