题目内容
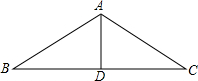如图，厂房屋顶人字架（△ABC为等腰三角形），AB=AC的跨度BC为10米，∠B=26°，求中柱AD（D为底边BC的中点）和上弦AB的长．（精确到0.01米）考点：解直角三角形的应用
专题：
分析：根据等腰三角形的性质得到DC=BD=5米，在Rt△ADC中，利用∠B的余弦进行计算即可得到AB．
解答：解：∵AB=AC，AD⊥BC，BC=10米，
∴DC=BD=5米，
在Rt△ADC中，∠B=26°，
∴tan26°=
，即AD=BD•tan26°≈2.44（米）．
cos26°=
，即AB=
≈6.67（米）．
答：中柱AD（D为底边BC的中点）为2.44米和上弦AB的长为6.67米．
∴DC=BD=5米，
在Rt△ADC中，∠B=26°，
∴tan26°=
| AD |
| BD |
cos26°=
| BD |
| AB |
| 5 |
| cos26° |
答：中柱AD（D为底边BC的中点）为2.44米和上弦AB的长为6.67米．
点评：本题考查了解直角三角形的应用：在直角三角形中，已知一个锐角和它的邻边，可利用这个角的余弦求出斜边．也考查了等腰三角形的性质．
练习册系列答案
相关题目
如图，AE∥DC，∠A=∠C，BD平分∠ADC，则下列说法不正确的是（ ）| A、AD∥BC |
| B、BC=DC |
| C、F为E中点 |
| D、AF=AD |
如图，在Rt△ABC中，∠C=90°，BC=3，AC=4，则sinA+sinB=
用“＞”或“＜”号填空：有理数a，b，c在数轴上对应的点如图：
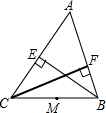如图，BE、CF是△ABC的高，M为BC的中点．试说明点B、C、E、F在以点M为圆心的同一圆上．