题目内容
3.计算:$\sqrt{16}÷\sqrt{2}-\sqrt{3}×(2-\sqrt{3})-\frac{3}{2}\sqrt{(-2)^{2}}$-$|1-\sqrt{2}|+\sqrt{\frac{1}{2}}-(1-\sqrt{3})^{2}$.分析 先进行二次根式的乘除运算和去绝对值得到原式=$\sqrt{16÷2}$-2$\sqrt{3}$+3-$\frac{3}{2}$×2+1-$\sqrt{2}$+$\frac{\sqrt{2}}{2}$-(1-2$\sqrt{3}$+3),然后合并即可.
解答 解:原式=$\sqrt{16÷2}$-2$\sqrt{3}$+3-$\frac{3}{2}$×2+1-$\sqrt{2}$+$\frac{\sqrt{2}}{2}$-(1-2$\sqrt{3}$+3)
=2$\sqrt{2}$-2$\sqrt{3}$+3-3+1-$\sqrt{2}$+$\frac{\sqrt{2}}{2}$-4+2$\sqrt{3}$
=$\frac{3\sqrt{2}}{2}$-3.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
14. 如图,∠A+∠B+∠C+∠D+∠E等于( )
如图,∠A+∠B+∠C+∠D+∠E等于( )
 如图,∠A+∠B+∠C+∠D+∠E等于( )
如图,∠A+∠B+∠C+∠D+∠E等于( )| A. | 180° | B. | 360° | C. | 540° | D. | 720° |
18.直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2),点C在直线AB上,且S△BOC=2,则点C的坐标是( )
| A. | (-2,-2) | B. | (-2,-6) | C. | (2,2) | D. | (2,2)或(-2,-6) |
15.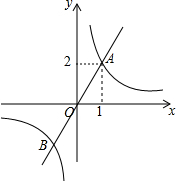 如图,函数y1=$\frac{k_1}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )
如图,函数y1=$\frac{k_1}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )
 如图,函数y1=$\frac{k_1}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )
如图,函数y1=$\frac{k_1}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )| A. | -1<x<0或x>1 | B. | x<-1或0<x<1 | C. | x>1 | D. | -1<x<0 |
20.下面有关三角形的内角的说法正确的是( )
| A. | 一个三角形中可以有两个直角 | |
| B. | 一个三角形的三个内角能都大于70° | |
| C. | 一个三角形的三个内角能都小于50° | |
| D. | 三角形中最大的内角不能小于60° |
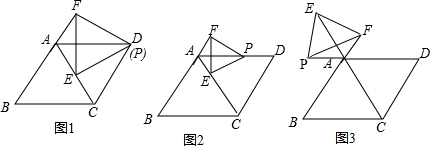
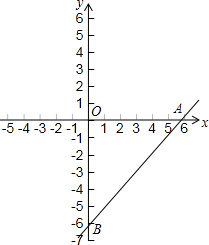 直线y=x-6与x轴、y轴分别交于A、B两点,点E从B点出发,以每秒1个单位长度的速度沿线段BO向O点移动(不考虑点E与B、O两点重合的情况),过点E作EF∥AB,交x轴于点F,将四边形ABEF沿直线EF折叠后,与点A对应的点记作点C,与点B对应的点记作点D,得到四边形CDEF,设点E的运动时间为t秒.
直线y=x-6与x轴、y轴分别交于A、B两点,点E从B点出发,以每秒1个单位长度的速度沿线段BO向O点移动(不考虑点E与B、O两点重合的情况),过点E作EF∥AB,交x轴于点F,将四边形ABEF沿直线EF折叠后,与点A对应的点记作点C,与点B对应的点记作点D,得到四边形CDEF,设点E的运动时间为t秒.