题目内容
20.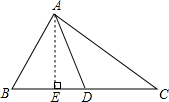 如图,AD是△ABC的中线,试说明:AB2+AC2=2(AD2+CD2)
如图,AD是△ABC的中线,试说明:AB2+AC2=2(AD2+CD2)
分析 利用勾股定理得AB2+AC2=2AD2-2ED2+BE2+CE2,进而由BE2=DC2+2DC•ED+ED2,CE2=DC2-2DC•ED+ED2,求出即可.
解答 证明:如图,作BC边上的高AE交BC于E, 则在Rt△ABE中,AB2=BE2+AE2,
则在Rt△ABE中,AB2=BE2+AE2,
在Rt△ACE中,AC2=CE2+AE2,
所以AB2+AC2=2AE2+BE2+CE2,
在在Rt△AED中,AE2=AD2-ED2,
则AB2+AC2=2AD2-2ED2+BE2+CE2,
∵AD是△ABC的BC边上的中线,
∴BD=DC,
∴BE2=(BD+ED)2=(DC+ED)2=DC2+2DC•ED+ED2,
CE2=(DC-ED)2=DC2-2DC•ED+ED2,
∴AB2+AC2=2AD2-2ED2+DC2+2DC•ED+ED2+DC2-2DC•ED+ED2,
∴AB2+AC2=2(AD2+CD2).
点评 本题考查勾股定理,三角形的中线及高的定义以及完全平方公式,关键是利用勾股定理得AB2+AC2=2AD2-2ED2+BE2+CE2.

练习册系列答案
相关题目
11.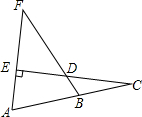 如图,C在AB延长线上,CE⊥AF于点E,交BF于点D,∠F=60°,∠C=20°,则∠FBA=( )
如图,C在AB延长线上,CE⊥AF于点E,交BF于点D,∠F=60°,∠C=20°,则∠FBA=( )
 如图,C在AB延长线上,CE⊥AF于点E,交BF于点D,∠F=60°,∠C=20°,则∠FBA=( )
如图,C在AB延长线上,CE⊥AF于点E,交BF于点D,∠F=60°,∠C=20°,则∠FBA=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
 如图,小岛C在小岛A的北偏东60°方向,在小岛B的北偏西45°方向,那么从C岛看A,B两岛的视角∠ACB的度数为105°.
如图,小岛C在小岛A的北偏东60°方向,在小岛B的北偏西45°方向,那么从C岛看A,B两岛的视角∠ACB的度数为105°.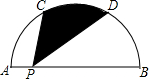 如图,半圆的直径AB=10,C、D是半圆的三等分点,P为AB上一点,求阴影部分的面积.
如图,半圆的直径AB=10,C、D是半圆的三等分点,P为AB上一点,求阴影部分的面积.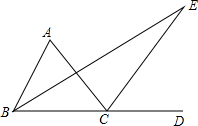 如图所示,在△ABC中,BE是∠ABC的平分线,CE是∠ACD的平分线,BE、CE交于点E,若∠A=68°,求∠E的度数.
如图所示,在△ABC中,BE是∠ABC的平分线,CE是∠ACD的平分线,BE、CE交于点E,若∠A=68°,求∠E的度数. 如图,求∠A+∠B+∠C+∠D+∠E-∠F-∠G的度数.
如图,求∠A+∠B+∠C+∠D+∠E-∠F-∠G的度数.