题目内容
8.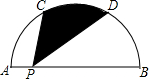 如图,半圆的直径AB=10,C、D是半圆的三等分点,P为AB上一点,求阴影部分的面积.
如图,半圆的直径AB=10,C、D是半圆的三等分点,P为AB上一点,求阴影部分的面积.
分析 连接CD、OC、OD,由点C,D为半圆的三等分点得出CD∥AB,故△OCD,△PCD是等底等高的三角形,根据S阴影=S扇形OCD即可得出结论.
解答  解:连接CD、OC、OD,
解:连接CD、OC、OD,
∵点C,D为半圆的三等分点,
∴CD∥AB,
∴△OCD,△PCD是等底等高的三角形,
∴阴影部分的面积就等于扇形OCD的面积.
∴S阴影=S扇形OCD=$\frac{60π×25}{360}$=$\frac{25π}{6}$.
点评 本题考查的是扇形面积的计算,根据题意作出辅助线,构造出面积相等的三角形是解答此题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
19.一次课堂练习,小颖同学做了如下4道因式分解题,你认为小颖做的不够完整的一道题是( )
| A. | x3-4x2+4x=x(x2+4x+4) | B. | x2y-xy2=xy(x-y) | ||
| C. | x2-y2=(x-y)(x+y) | D. | x2-2xy+y2=(x-y)2 |
18.在平面内有A、B两点,若以B点为原点建立平面直角坐标系,则点A的坐标为(2,5),若以A点为原点建立平面直角坐标系,则点B的坐标为( )
| A. | (-2,-5) | B. | (-2,5) | C. | (2,-5) | D. | (2,5) |
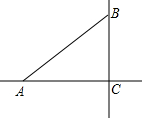 如图,在△ABC中,∠ACB=90°,∠BAC=40°,在直线AC上找点P,使△ABP是等腰三角形,则∠APB的度数为20°或40°或70°或100°.
如图,在△ABC中,∠ACB=90°,∠BAC=40°,在直线AC上找点P,使△ABP是等腰三角形,则∠APB的度数为20°或40°或70°或100°.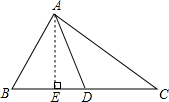 如图,AD是△ABC的中线,试说明:AB2+AC2=2(AD2+CD2)
如图,AD是△ABC的中线,试说明:AB2+AC2=2(AD2+CD2)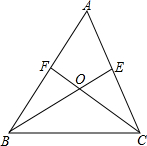 如图,在△ABC中,BE平分∠ABC,F是AB边上一点,CF交BE于点O,∠BOC=90°+$\frac{1}{2}$∠A,请你用推理的方法说明CF平分∠ACB.
如图,在△ABC中,BE平分∠ABC,F是AB边上一点,CF交BE于点O,∠BOC=90°+$\frac{1}{2}$∠A,请你用推理的方法说明CF平分∠ACB.