题目内容
12．在Rt△ABC中，∠C=90°，∠A=30°，AB=2，则△ABC的周长是3+$\sqrt{3}$（结果保留根号）分析 在直角三角形ABC中，利用含30度直角三角形的性质得到BC=$\frac{1}{2}$AB，求出BC的长，再利用勾股定理求出AC的长，即可求出三角形ABC周长．
解答 
解：∵在Rt△ABC中，∠C=90°，∠A=30°，AB=2，
∴BC=$\frac{1}{2}$AB=1，
根据勾股定理得：AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{3}$，
则△ABC周长为3+$\sqrt{3}$，
故答案为：3+$\sqrt{3}$
点评 此题考查了含30度直角三角形的性质，以及勾股定理，熟练掌握性质及定理是解本题的关键．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
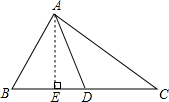如图，AD是△ABC的中线，试说明：AB2+AC2=2（AD2+CD2）
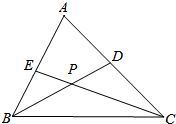如图，在△ABC中，BD、CE分别是∠ABC，∠ACB的平分线．
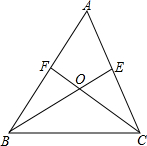如图，在△ABC中，BE平分∠ABC，F是AB边上一点，CF交BE于点O，∠BOC=90°+$\frac{1}{2}$∠A，请你用推理的方法说明CF平分∠ACB．
如图，在△ABC中，∠C=40°，∠B=80°，AD平分∠CAB，求：
根据数轴，解答下列问题：