题目内容
15.当a为何值时,方程$\frac{1}{4}$x2-(2a+1)x+4a2-1=0.(1)有两个不相等的实数根?
(2)有两个相等的实数根?
(3)没有实数根?
分析 先求出△=[-(2a+1)]2-4×$\frac{1}{4}$×(4a2-1)=4a+2;
(1)由△>0,解关于m不等式求出m的范围;
(2)由△=0,解关于m的方程求出m的值;
(3)由△<0,解关于m的不等式求出m的范围.
解答 解:△=[-(2a+1)]2-4×$\frac{1}{4}$×(4a2-1)=4a+2;
(1)当△>0,方程有两个不相等的实数根;
即4a+2>0,所以>-$\frac{1}{2}$;
(2)当△=0,方程有两个相等的实数根;
即4a+2=0,所以a=-$\frac{1}{2}$;
(3)当△<0,方程没有实数根;
即<0,所以a<-$\frac{1}{2}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了不等式的解法.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
5. 如图是小强画出的一张脸的简笔画,他对小刚说:“我用(0,2)表示左眼的位置,用(2,2)表示右眼的位置,”那么嘴的位置可表示成( )
如图是小强画出的一张脸的简笔画,他对小刚说:“我用(0,2)表示左眼的位置,用(2,2)表示右眼的位置,”那么嘴的位置可表示成( )
 如图是小强画出的一张脸的简笔画,他对小刚说:“我用(0,2)表示左眼的位置,用(2,2)表示右眼的位置,”那么嘴的位置可表示成( )
如图是小强画出的一张脸的简笔画,他对小刚说:“我用(0,2)表示左眼的位置,用(2,2)表示右眼的位置,”那么嘴的位置可表示成( )| A. | (1,0) | B. | (-1,0) | C. | (0,1) | D. | (1,-1) |
10.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(a,b),则经过第2014次变换后所得A点坐标是( )
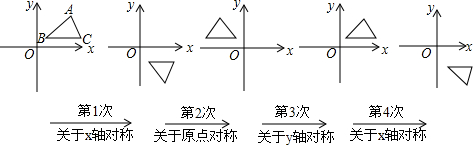

| A. | (a,-b) | B. | (-a,-b) | C. | (-a,b) | D. | (a,b) |
 如图,在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABD的周长为20cm,AE=5cm,则△ABC的周长是30cm.
如图,在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABD的周长为20cm,AE=5cm,则△ABC的周长是30cm.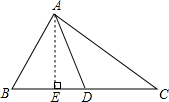 如图,AD是△ABC的中线,试说明:AB2+AC2=2(AD2+CD2)
如图,AD是△ABC的中线,试说明:AB2+AC2=2(AD2+CD2)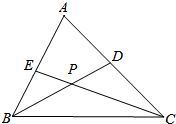 如图,在△ABC中,BD、CE分别是∠ABC,∠ACB的平分线.
如图,在△ABC中,BD、CE分别是∠ABC,∠ACB的平分线. 如图,在△ABC中,∠C=40°,∠B=80°,AD平分∠CAB,求:
如图,在△ABC中,∠C=40°,∠B=80°,AD平分∠CAB,求: 如图,已知△ABC的面积为21cm2,CD是△ABC的高,若CD=6cm,则AB=7cm.
如图,已知△ABC的面积为21cm2,CD是△ABC的高,若CD=6cm,则AB=7cm.