题目内容
3.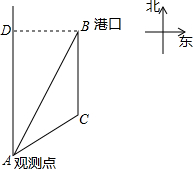 已知B港口位于A观测点北偏东30°方向,且其到A观测点正北方向的距离BD的长为16km,一艘货轮从B港口以40km/h的速度沿如图所示的BC方向航行,30min后达到C处,现测得C处位于A观测点北偏东60°方向,则此时货轮与A观测点之间的距离AC的长是(16$\sqrt{3}$-12)km.
已知B港口位于A观测点北偏东30°方向,且其到A观测点正北方向的距离BD的长为16km,一艘货轮从B港口以40km/h的速度沿如图所示的BC方向航行,30min后达到C处,现测得C处位于A观测点北偏东60°方向,则此时货轮与A观测点之间的距离AC的长是(16$\sqrt{3}$-12)km.
分析 过点B作BE垂直于AC延长线于点E,在Rt△ABD中求得AB=2BD=32,在Rt△BAE中求得AE=ABcos∠BAE=16$\sqrt{3}$km、BE=ABsin∠BAE=16,利用勾股定理求得CE=12,根据AC=AE-CE可得答案.
解答 解:如图,过点B作BE垂直于AC延长线于点E,
在Rt△ABD中,∵∠BAD=30°,BD=16km,
∴AB=2BD=32km,
∵∠BAE=∠CAD-∠BAD=30°,
∴AE=ABcos∠BAE=32×$\frac{\sqrt{3}}{2}$=16$\sqrt{3}$km,BE=ABsin∠BAE=16,
∴CE=$\sqrt{B{C}^{2}-B{E}^{2}}$=12,
则AC=AE-CE=16$\sqrt{3}$-12(km),
故答案为:(16$\sqrt{3}$-12)km.
点评 本题主要考查解直角三角形的应用,根据已知构造直角三角形得出BE的长是解题关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
18. 如图,AD、AC分别为⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,BO=5,则CD的长为( )
如图,AD、AC分别为⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,BO=5,则CD的长为( )
 如图,AD、AC分别为⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,BO=5,则CD的长为( )
如图,AD、AC分别为⊙O的直径和弦,∠CAD=30°,B是AC上一点,BO⊥AD,垂足为O,BO=5,则CD的长为( )| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 5$\sqrt{3}$ |
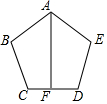 如图,已知AB=AE,∠ABC=∠AED,BC=ED,点F是CD的中点,连接A,F.AF与CD有怎样的关系?并说明理由.
如图,已知AB=AE,∠ABC=∠AED,BC=ED,点F是CD的中点,连接A,F.AF与CD有怎样的关系?并说明理由. 如图,数轴上的点P表示的数是-1,将点P向左平移1个单位长度再向右平移9个单位长度后得到点P′,则点P平移经过了8个非负整数点.
如图,数轴上的点P表示的数是-1,将点P向左平移1个单位长度再向右平移9个单位长度后得到点P′,则点P平移经过了8个非负整数点.