题目内容
14．在直角三角形ABC中，∠C=60°，以AB为直径的半圆交斜边BC于D，则△ACD与△ABD的面积之比为（ ）| A． | 1：2 | B． | 1：3 | C． | 2：3 | D． | 3：4 |
分析 由AB是直径，推出∠ADB=∠ADC=90°，由∠CAB=90°，∠C=60°，推出∠CAD=∠B=30°，设CD=a，则AC=2CD=2a，BC=2AC=4a，推出BD=3a，根据S△ACD：S△ABD=CD：DB即可解决问题．
解答 解：如图，∵AB是直径，
∴∠ADB=∠ADC=90°，
∵∠CAB=90°，∠C=60°，
∴∠CAD=∠B=30°，设CD=a，则AC=2CD=2a，BC=2AC=4a，
∴BD=3a，
∴S△ACD：S△ABD=CD：DB=1：3．
故选B．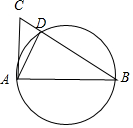
点评 本题考查圆的有关知识，直角三角形30度角性质、三角形的面积等知识，解题的关键是学会利用参数解决问题，属于中考常考题型．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
如图，在平面直角坐标系中，抛物线与x轴交于点A（-1，0）和点B（1，0），直线y=2x-1与y轴交于点C，与抛物线交于点C、D．