题目内容
6.已知点A(4,m),B( n,-8)在反比例函数y=$\frac{8}{x}$的图象上,设直线AB与x轴交于点C.(1)求点C的坐标.
(2)如果点D在y轴上,且使△BCD为直角三角形,则符合要求的点D共有4个.
分析 (1)将A(4,m),B( n,-8)分别代入反比例函数的解析式y=$\frac{8}{x}$得m=2,n=-1,求得A(4,2),B(-1,-8),得到直线AB解析式为y=2x-6,即可得到结果;
(2)设D(0,m),当∠BCD=90°时,当∠BDC=90°时,当∠DBC=90°时,根据勾股定理分别列方程求解,即可求得结论.
解答 解:(1)将A(4,m),B( n,-8)分别代入反比例函数的解析式y=$\frac{8}{x}$得m=2,n=-1,
∴A(4,2),B(-1,-8),
设直线AB的解析式为y=kx+b,
将A与B坐标代入得:$\left\{\begin{array}{l}{4k+b=2}\\{-k+b=-8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=-6}\end{array}\right.$.
故直线AB解析式为y=2x-6,
令y=0,得到x=3,
即C(3,0);
(2)∵点D在y轴上,
∴设D(0,m),
则CD2=32+m2,
BC2=(1+3)2+82=80,
BD2=12+(m+8)2,
∵△BCD为直角三角形,
∴当∠BCD=90°时,则有BD2=CD2+BC2,
即12+(m+8)2=32+m2+80,
解得:m=$\frac{3}{2}$,
∴D(0,$\frac{3}{2}$),
当∠BDC=90°时,则有BC2=CD2+BD2,
即80=32+m2+12+(m+8)2,
解得:m=4±$\sqrt{19}$,
∴D(0,4+$\sqrt{19}$),(0,4-$\sqrt{19}$),
当∠DBC=90°时,则有DC2=BC2+BD2,
即32+m2=80+12+(m+8)2,
解得m=$\frac{17}{2}$,
∴D(0,$\frac{17}{2}$),
∴符合要求的点D共有4个.
故答案为:4.
点评 此题考查了一次函数与反比例函数的交点问题,待定系数法求函数的解析式,直角三角形的性质,熟练掌握待定系数法是解本题的关键.

| A. | $\frac{2}{3}$ | B. | $\frac{1}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$ |
| A. | -6 | B. | -$\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | 6 |
| A. | 2a2•3a3=6a6 | B. | 2xa+xa=3x2a2 | C. | (-2a)3=-6a3 | D. | a5÷a4=a |
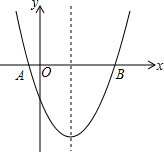 如图,已知抛物线y=x2-3x-$\frac{7}{4}$与x轴交于A、B两点.
如图,已知抛物线y=x2-3x-$\frac{7}{4}$与x轴交于A、B两点.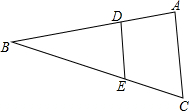 如图,在△ABC中,点D、点E分别在AB、BC边上,且DE∥AC,DE=2,AC=3,BE=4,则BC长度为6.
如图,在△ABC中,点D、点E分别在AB、BC边上,且DE∥AC,DE=2,AC=3,BE=4,则BC长度为6.