题目内容
14.计算:|tan45°-2|-(3.14-π)0+$\sqrt{8}$×(-$\frac{1}{2}$)-2.分析 原式第一项利用特殊角的三角函数值及绝对值的代数意义化简,第二项利用零指数幂法则计算,第三项利用负整数指数幂法则计算即可得到结果.
解答 解:原式=|1-2|-1+2$\sqrt{2}$×4=1-1+8$\sqrt{2}$=8$\sqrt{2}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
2.已知3x=4y(x≠4),则下列各式不成立的是( )
| A. | $\frac{x}{3}$=$\frac{y}{4}$ | B. | $\frac{x+4}{4}$=$\frac{y+3}{3}$ | C. | $\frac{x+y}{4+3}$=$\frac{x}{4}$ | D. | $\frac{4-x}{x}$=$\frac{3-y}{y}$ |
19. 如图,点O为数轴原点,则数轴上表示互为相反数的点是( )
如图,点O为数轴原点,则数轴上表示互为相反数的点是( )
 如图,点O为数轴原点,则数轴上表示互为相反数的点是( )
如图,点O为数轴原点,则数轴上表示互为相反数的点是( )| A. | 点A和点C | B. | 点C和点D | C. | 点A和点D | D. | 点B和点D |
3.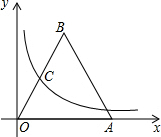 如图,等边三角形OAB的一边OA在x轴上,双曲线y=$\frac{\sqrt{3}}{x}$在第一象限内的图象经过OB边的中点C,则点B的坐标是( )
如图,等边三角形OAB的一边OA在x轴上,双曲线y=$\frac{\sqrt{3}}{x}$在第一象限内的图象经过OB边的中点C,则点B的坐标是( )
 如图,等边三角形OAB的一边OA在x轴上,双曲线y=$\frac{\sqrt{3}}{x}$在第一象限内的图象经过OB边的中点C,则点B的坐标是( )
如图,等边三角形OAB的一边OA在x轴上,双曲线y=$\frac{\sqrt{3}}{x}$在第一象限内的图象经过OB边的中点C,则点B的坐标是( )| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,1) | C. | (2,2$\sqrt{3}$) | D. | (2$\sqrt{3}$,2) |
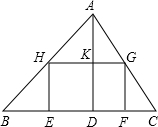 如图,在△ABC中,AD是BC边上的高,BC=12,AD=8,矩形EFGH的边EF与BC重合,点G、H分别在AC、AB上运动.
如图,在△ABC中,AD是BC边上的高,BC=12,AD=8,矩形EFGH的边EF与BC重合,点G、H分别在AC、AB上运动.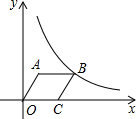 如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则反比例函数的表达式为y=$\frac{32}{x}$(x>0).
如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则反比例函数的表达式为y=$\frac{32}{x}$(x>0).