题目内容
1.有3张背面相同的卡片,正面分别印有下列几种几何图形.现将这3张卡片正面朝下摆放,从中任意抽取一张后放回,再从中任意抽取一张,则两次抽到的卡片的正面图形都是中心对称图形的概率是( )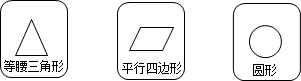
| A. | $\frac{2}{3}$ | B. | $\frac{1}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$ |
分析 可以采用树状图求解.此题为不放回实验,共有9种情况,摸出两张牌面图形都是中心对称图形的纸牌的有4种,所以摸出两张牌面图形都是中心对称图形的纸牌的概率是$\frac{4}{9}$.
解答 解:设A是等腰三角形,B是平行四边形,C是圆,
画树状图得,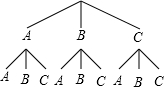
∴一共有9种情况,
∵B与C时中心对称图形,
∴摸出两张牌面图形都是中心对称图形的纸牌有4种;
∴摸出两张牌面图形都是中心对称图形的纸牌的概率是$\frac{4}{9}$.
故选:C.
点评 此题主要考查了树状图法求概率,树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.下列运算中,正确的运算是( )
| A. | a3+a3=a6 | B. | $\sqrt{9}$-$\sqrt{5}$=$\sqrt{4}$ | C. | $\sqrt{(-3)^{2}}$=3 | D. | (a-b)2=a2-b2 |
13. 如图,菱形ABCD的对角线相交于点O,若AC=12,AB=7,则BD的长为( )
如图,菱形ABCD的对角线相交于点O,若AC=12,AB=7,则BD的长为( )
 如图,菱形ABCD的对角线相交于点O,若AC=12,AB=7,则BD的长为( )
如图,菱形ABCD的对角线相交于点O,若AC=12,AB=7,则BD的长为( )| A. | $\sqrt{13}$ | B. | 6 | C. | 2$\sqrt{13}$ | D. | 10 |
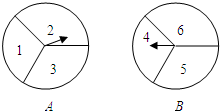 如图所示.有两个自由转动的均匀转盘A,B,都被分成了3等份,
如图所示.有两个自由转动的均匀转盘A,B,都被分成了3等份, 如图,l是直线y=x-4的图象,点P(1,m)在该直线的上方,则m的取值范围是m>-3.
如图,l是直线y=x-4的图象,点P(1,m)在该直线的上方,则m的取值范围是m>-3.