题目内容
16.若抛物线y=x2+(a-1)x+a+2的顶点在坐标轴上,则a的值为1或-1或7.分析 当顶点在y轴上时,则对称轴为x=0,由对称轴方程可求得a的值;当顶点在x轴上时,y=0时的方程有两个相等的实数根,可求得a的值.
解答 解:
当顶点在y轴上时,则对称轴为x=0,
∴-$\frac{a-1}{2}$=0,解得a=1;
当顶点在x轴上时,令y=0可得,x2+(a-1)x+a+2=0有两个相等的实数根,
∴△=0,即(a-1)2-4(a+2)=0,解得a=7或a=-1;
综上可知a的值为1或-1或7,
故答案为:1或-1或7.
点评 本题主要考查二次函数的顶点坐标,分两种情况分别确定a的值是解题的关键.

练习册系列答案
相关题目
12.不等式-3x<6的解集为( )
| A. | x<-2 | B. | x>-2 | C. | x<2 | D. | x>2 |
8.实数4的倒数是( )
| A. | 4 | B. | $\frac{1}{4}$ | C. | -4 | D. | -$\frac{1}{4}$ |
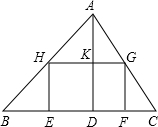 如图,在△ABC中,AD是BC边上的高,BC=12,AD=8,矩形EFGH的边EF与BC重合,点G、H分别在AC、AB上运动.
如图,在△ABC中,AD是BC边上的高,BC=12,AD=8,矩形EFGH的边EF与BC重合,点G、H分别在AC、AB上运动.
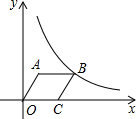 如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则反比例函数的表达式为y=$\frac{32}{x}$(x>0).
如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则反比例函数的表达式为y=$\frac{32}{x}$(x>0).